Young’s double slit experiment:- (For interference light)

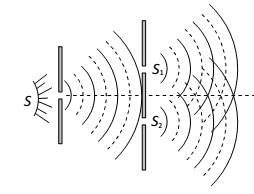
A mono chromatic source of light illuminates the slit S which sends out spherical wave fronts. These wave fronts reach S₁ and S₂ simultaneously which become the source of secondary wavelets.

When light waves from S₁ and S₂ arrive in phase (crest falls on crest & trough fall on through), constructive interference takes place and a bright band is formed on the screen.

When light waves arrive out of phase (crest falls on trough), destructive interference takes place and a dark band is formed on the screen.

Interference Fringes:- The alternate dark and bright bands on the screen are called as “interference fringes.”

Fringe width (β):- the distance between two successive dark or bright bands is called as “fringe width”.

Central maxima: the point ‘O’ on the screen at which the intensity of light is maximum, is called as central maxima.

Theory of Interference:-

Step-I:- To find the equation of resultant wave:

Let the displacements of the waves from two light sources are:

y₁ = a₁ sin wt

y₂ = a₂ sin (wt + φ)

Where

a₁, a₂ => Amplitudes of two waves

φ => constant phase difference by which 2^nd wave leads the first.

According to superposition principle, the displacement of resultant wave is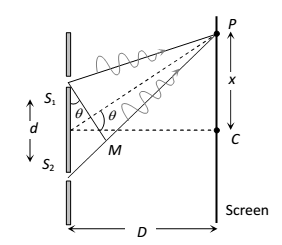

y = y₁ + y₂ = a₁ sin wt + a₂ sin (wt + φ)

y = a₁ sin wt + a₂ [ sin wt cos φ + cos wt sin φ]

y = (a₁ + a₂ cos φ) sin wt + a₂ sin φ cos wt

y = A cons θ sin wt + A sin θ cos wt

let           a₁ + a₂ cos φ = A cos θ ---------- (1)

&             a₂ sin φ = A sin θ -----------------(2)

y = A sin (wt + θ)              [S.H.M equation]

Thus the resultant wave is a simple harmonic wave of amplitude A.

Step- II:-

Since     A cos θ = a₁ +a₂ cos φ

                A sin θ = a₂ sin φ

Squaring and adding

A² = a₁² + a₂² cos² φ + 2a₁ a₂ cos φ + a₂² sin² φ

A² = a₁² + a₂² (cos² φ + sin² φ) + 2a₁ a₂ cos φ

Step- III:-

To find the resultant Intensity:-

To find the resultant Intensity:-

Resultant intensity (I) at P ∝ (Amplitude)² of resultant wave

∴ I ∝ A²                or            I = KA²

Or           I = K (a₁² + a₂² + 2a₁ a₂ cos φ)

                I = K a₁² + K a₂² + 2K a₁ a₂ cos φ   ------------ (1)

Intensity of individual waves, I₁ = K a₁²   &             I₂ = K a₂²

∴ from (1)

Step IV:-

Conditions for constructive interference: (conditions of maxima)

Since

For constructive interference, I is maximum.

                                                      ∴ cos φ = maximum = +1

                                                      ∴ φ = 0, 2π, 4, ------------

i.e.                                                φ = 2nπ           n=0,1,2,3 -----------

path difference between the two waves reaching at point ‘P’ corresponding to phase difference φ is

Therefore interference will be constrictive (max. intensity) it the path difference between the waves is an integral multiple or λ.

Step V:

Condition for destructive interference: (condition of minima )

I is minimum ∴ cos φ = minimum = -1

                                                      = φ = π, 3 π, 5 π,-----------

                                                      Or  φ = (2n + 1) π        n=1,2,3,------------

Path difference between the waves corresponding to a phase difference φ is

∴ interference will be destructive min. intensity if the path difference between the waves is an odd integral multiple  of λ/2.

Step VI:

Ratio of maximum and minimum intensity of light:

Since                                           I = K (a₁² + a₂² + 2a₁ a₂ cos φ)

I = I max. when cos φ = +1

∴  I max. = K (a₁² + a₂² + 2a₁ a₂)

                = K (a₁ + a₂)²

I = I min. when cos φ = -1

I min. = K (a₁² + a₂² - 2a₁ a₂)

= K (a₁ - a₂)²

Step VII:-

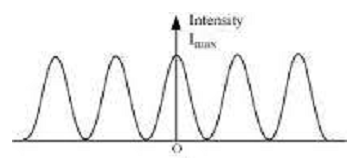
Intensity distribution curve of interference pattern:

The resultant intensity due to super position of two waves having constant phase difference φ is

If I₁ = I₂ = I₀, then I = 2 I₀ + 2 I₀ cos φ = 2 I₀(1 + cos φ)

For Maxima:                            φ = 2n π          where n=0,1,2,3, --------

                                                      φ = 0, 2π, 4π, 6π,------------

                                                      ∴ I = 2 I₀(1+1)               I =4I₀      I₀ = intensity of individual wave

For minima:                             φ = (2n+1) π where n = 0,1,2,3, --------

                                                      ∴ φ = π, 3π, 5π ------------, I = 2I₀ (1-1)

                                                      I = 0

i.e. all the Maxima ( Bright fringes ) are of constant intensity (4I₀) and the Minima ( dark fringes ) are of ‘Zero’ intensity i.e. totally dark.

step VIII:-

Relation between intensity and width of source Intensity of light ∝ width of source:

let W₁, W₂ => width of two sources S₁ and S₂

_{∴ I1 ∝ W1   &    I2 ∝ W2}

 ∴ I ∝ (amplitude)²

∴ I₁∝ a₁²

   I₂∝ a₂²