# Refraction at convex spherical surface:

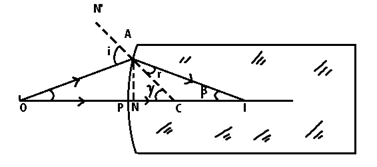
(a) When the object lies in the rarer medium and image formed is real:

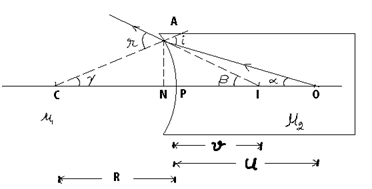
Consider a spherical refracting surface (convex) of refraction index µ₂. Let an object O is placed in a rarer medium of refraction index µ₁.

A ray of light incident normally on the surface passes un deviated while the other ray which is incident at < i is refracted & bends towards the normal. At point I, a real image of O is formed.

Step I In ΔOAC, ∝ + (180 – i) + γ = 180 ==>  i = ∝ + γ      —(1)

In ΔIAC, r + β + (180 – γ) = 180 ==>  r = γ - β                      —(2)

Angles ∝, β, γ and small tan ∝ = ∝    

Step II, Now tan ∝ = (AN/NO) = (AN/PO) = (AN/-u)     or      ∝ = AN/-u   —(3)

tan β = (AN/NI) = (AN/PI) = (AN/υ)           or      β = AN/υ      —(4)

tan γ = (AN/NC) = (AN/PC) = (AN/R)        or      γ = AN/R      —(5)

Step III, Acc. to Snell’s law at pt. A

i & r are small ∴ sin i = i, sin r = r

sin i/sin r = ¹µ₂ = µ₂/µ₁

µ₁ sin i = µ₂ sin r

µ₁ i = µ₂ r

µ₁(∝ + γ) = µ₂(γ - β)        [using (1) & (2)

µ₁ ∝ + µ₁ γ = µ₂ γ - µ₂ β

µ₁ ∝ + µ₂ β = µ₂ γ - µ₁ γ

µ₁ (AN/-u) + µ₂ (AN/υ) = (µ₂ - µ₁) (AN/R)         [using 3, 4, 5]

∴ (-µ₁/u) + (µ₂/υ) = (µ₂ - µ₁/R)

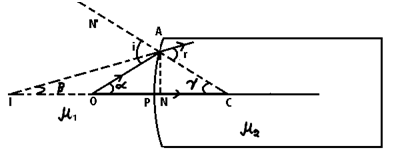
(b) When the object lies in the rarer medium and the image formed is virtual:

Let o → Point object placed on principle axis and lying close to the pole of the refracting surface.

In ΔOAC, ∝ + (180 – i) + γ = 180

i = ∝ + γ

In ΔIAC, β + (180 – r) + γ = 180

r = β + γ

Now tan ∝ = (AN/NO) = (AN/PO) = (AN/-u)       or      ∝ = (AN/-u)

tan β = (AN/NI) = (AN/PI) = (AN/-υ)         or      β = (AN/-υ)

tan γ = (AN/NC) = (AN/PC) = (AN/R)        or      γ = AN/R     

By Snell’s law at A,

sin i/sin r = (µ₂/µ₁) or µ₁ sin i = µ₂ sin r

Or µ₁ i = µ₂ r

Or µ₁ (∝ + γ) = µ₂ (β + γ)

Or µ₁ ∝ + µ₁ γ = µ₂ β + µ₂ γ

Or µ₁ ∝ - µ₂ β = (µ₂ - µ₁) γ

Or µ₁.(AN/-u) - µ₂.(An/-υ) = (µ₂ - µ₁)AN/R

Or (-µ₁/u) + (µ₂/υ) = (µ₂ - µ₁)/R

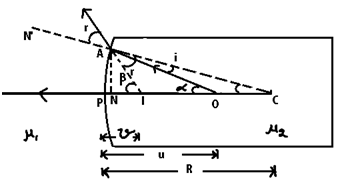
(c) When the object lies in the denser medium:

Let o Δ Point object lying in the denser medium

A ray of light from the object falling normally on the refracting surface passes undeviated. Another ray falling at pt. A bends away from the normal. The two rays appear to come from point I. ∴I is the virtual image of point object O.

In ΔOAC, i + (180^° – ∝) + γ = 180^° ==>  i = ∝ - γ

In ΔIAC, r + (180^° – β) + γ = 180^° ==>  r = β - γ

PO = -u

the distance of object is measured against the incident ray

Now tan ∝ = (AN/NO) = (AN/PO) = (AN/-u)       or      ∝ = (AN/-u)

tan β = (AN/NI) = (AN/PI) = (AN/-υ)         or      β = (AN/-υ)

tan γ = (AN/NC) = (AN/PC) = (AN/-R)       or      γ = AN/-R   

By Snell’s law at pt. A,

sin i/sin r = ²µ₁ = (µ₁/µ₂) or µ₂ i = µ₁ r

Or µ₂ (∝ - γ) = µ₂ (β - γ)

Or µ₂ ∝ - µ₂ γ = µ₁ β - µ₁ γ)

Or µ₂ ∝ - µ₁ β = (µ₂ - µ₁) γ

Or µ₂.(AN/-u) - µ₁.(AN/-υ) = (µ₂ - µ₁) (AN/-R)

Or (-µ₂/u) + (µ₁/υ) = (µ₁ - µ₂)/R

Note- If we know the relation for light rays from rarer → denser

Then the relation for light ray from denser → rarer can be obtained by replacing µ₂ by µ₁ & µ₁ by µ₂.

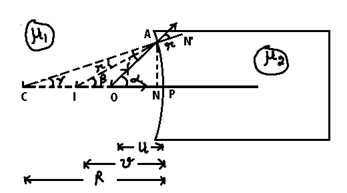
# Refraction at a concave spherical surface:

(Note: A virtual image is formed always in a concave S.R.S)

(a) When the object lies in the rarer medium:

Let o → Point object lying in the rarer medium and situated on the principal axis.

In ΔOAC, i + (180^° – ∝) + γ = 180^° ==>  i = ∝ - γ

In ΔIAC, r + (180^° – β) + γ = 180^° ==>  r = β - γ

Now tan ∝ = (AN/NO) = (AN/PO) = (AN/-u)       or      ∝ = (AN/-u)

tan β = (AN/NI) = (AN/PI) = (AN/-υ)         or      β = (AN/-υ)

tan γ = (AN/NC) = (AN/PC) = (AN/-R)       or      γ = AN/-R

By Snell’s law at A, (sin i/ sin r) = ¹µ₂ = µ₂/µ₁

Or µ₁ sin i = µ₂ sin r

Or µ₁ i = µ₂ r

Or µ₁ (∝ - γ) = µ₂ (β - γ)

Or µ₁ ∝ - µ₁ γ = µ₂ β - µ₂ γ

Or µ₁ ∝ - µ₂ β = (µ₁ - µ₂) γ

Or µ₁.(AN/-u) - µ₂.(AN/-υ) = (µ₁ - µ₂)AN/-R

Or (-µ₁/u) + (µ₂/υ) = µ₂ - µ₁/R

(b) When the object lies in the denser medium:

Let o → Point object lying in the denser medium 

In ΔOAC, ∝ + (180^° - i) + γ = 180^°

i = ∝ + γ

In ΔIAC,

β + (180^° - r) + γ = 180^°

r = β + γ

Now tan ∝ = (AN/NO) = (AN/PO) = (AN/-u)       or      ∝ = (AN/-u)

tan β = (AN/NI) = (AN/PI) = (AN/-υ)         or      β = (AN/-υ)

tan γ = (AN/NC) = (AN/PC) = (AN/R)        or      γ = AN/R

By Snell’s law at A,

  (sin i/sin r) = ²μ₁ = (μ₁/μ₂)

Or       μ₂ i = μ₁ r

Or       μ₂ (∝ +γ) = μ₁ (β+γ)

Or       μ₂ ∝ + μ₂γ = μ₁β+ μ₁ γ

Or       μ₂ ∝ - μ₁β = (μ₁- μ₂) γ 

Or       μ₂.(AN/-u)- μ₁(AN/-v) = (μ₁- μ₂)AN/R

Or      (-μ₂/u)+ (μ₁/v) = ((μ₁- μ₂)/R)

Note: (i) When the object lies in the rarer medium, then both convex & concave faces, the formula is

(-µ₁/u) + (µ₂/v) = (µ₂ - µ₁/R)

(ii) When object lies in denser medium, the for molar become

(µ₂/u) + (µ₁/v) = (µ₁ - µ₂/R)