Prism
# Prism:
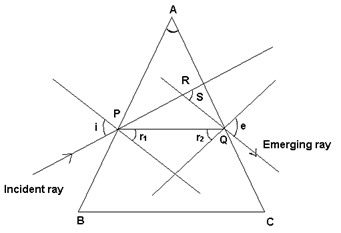
A simple prism is a transparent medium bounded by two triangular and three rectangular surfaces.
# Refraction through a prism:
A ray of light incident on the face AB of the prism is refracted and bends towards the normal. The refracted ray PQ is incident on the face AC. After refraction at point Q, it bends away from the normal.
i → angle of incidence, e → angle of emergence
δ → angle of deviation (angle between incident ray and emergent ray)
µ → Refractive index of glass prism w.r.t. air.
(a) To prove i + e = A + δ
In Δ APQ:
A + (90 – r1) + (90 – r2) = 180
==> r1 + r2 = A
In Δ RPQ:
(180 – δ) + (i – r1) + (e – r2) = 180
==> i + e = A + δ H.P.
∴ Sum of angle of incidence and angle of emergence
= Sum of angle of prism and angle of deviation.
(b) Relation between δ, µ and A: To prove: δ = (µ - 1) A
According to Snell’s law at point P;
µ = sin i/sin r1 = i/r1 ==> i = µ r1
According to Snell’s law at point Q;
1/µ = sin r2/sin e = r2/e ==> e = µ r2
Putting the values of i and e in i + e = A + δ
µ r1 + µ r2 = A + δ
µ (r1 + r2) = A + δ
µ A = A + δ
==> δ = (µ - 1) A
Note:-
(i) We have A + δ = i + e
∴ δ depends upon i
If the angle of incidence (i) is increased gradually, the angle of deviation (δ) first decreases, attains a minimum value (δm) and the starts increasing. When the angle of deviation is minimum, the prism is said to be in minimum deviation position.
(ii) There are two values of angle of incidence (i1, i2) for which δ is same.
(iii) Angle of minimum deviation (δm):
“The minimum value of angle of deviation for a prism is called as angle of minimum deviation.”
(c) Prism formula:
We have i + e = A + δ —(1)
And r1 + r2 = A —(2)
When δ = δm: (Prism in minimum deviation position)
Then e = i & r1 = r2 = r (say)
∴ Equation (1) ==> i + i = A + δm ==> i = A + δm/2
Equation (2) ==> r + r = A ==> r = A/2
According to Snell’s law at P;
µ = sin i/sin r1 = sin i/sin r ( r1 = r)
µ = sin (A + δm/2)/(sin A/2) (Prism formula)
 SureDen
SureDen