# Practical applications of refraction:

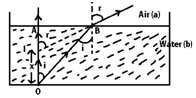
(1) The apparent depth of objects is lesser in denser medium than the actual depth:

Let O → pt. object at the actual depth OA

Any ray incidenting normally along OA goes straight while another ray incidenting alogn OB bends away from the normal after refraction. On producing back, the ray meets at point I.                

∴ I → virtual image of O. & hence IA → APP  

                                                                 OA → Real

By Snell’s law at B: ^bµ_a = (sin i/sin r)

Or 1/^aµ_b = (sin i/sin r)

Or ^aµ_b = (sin r/sin i)            —(1)

In Δ OAB, sin I = (AB/OB), In Δ IAB sin r = AB/IB

Putting in (1), ^aµ_b = (AB/IB)/(AB/OB) = (OB/IB) = (OA/IA)     [ i & r small ∴ OB = OA IB = IA]

∴ ^aµ_b = OA/IA = Real depth/Apparent depth

Normal shift (x):

Normal shift in the position of object, x = OA – IA

x = OA (1 – IA/OA) = OA (1 - 1/ ^aµ_b)

In general: x = d(1 – 1/ ^aµ_b)

d → real depth

µ → absolute refraction index of metal

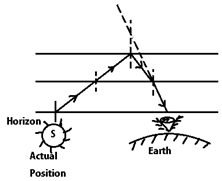
(ii) Apparent shift in the position of the sum at sunset and sunset:

The light rays from the sum (s) undergo refraction continuously and deviate more and more away from the normal.                      

To an observer (0), the sum appears at s’ (above the horizon)

Hence the sum appears to rise few minutes (2 minutes) before the actual sun rise and continues to appear few minutes (2 minutes) later after actual sun-set. ∴ Day becomes longer by about 4 minutes due to refraction.

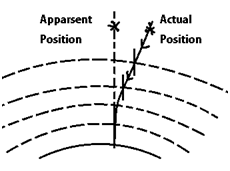
(iii) Twinkling of stars:                 

Light emitted by the stars is refracted continuously by the different layers of atmosphere. Before it reaches the earth, So the apparent position of the star is different from its actual position. Since the temperature and density of atmosphere keep on changing continuously, so the apparent position of the star also keep on changing continuously. This change in the apparent position of star leads to the twinkling of a star.

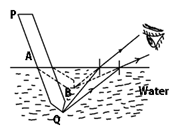
(iv) A pencil appears bent in water:

The rays of light from point Q of a pencil bends away from the normal after refraction at the surface of water

The refracted rays appear to come from point B. so AQ portion of pencil dipped in water appears as AB. ∴ The portion of pencil dipped in water appears to be bent.