# Power of a lens (P):  

It is the ability of a lens to converge or diverge a beam of light falling on it.

Mathematically:

Power is equal to reciprocal of focal length i.e. P = 1/f

For a convex lens: P is positive         ( f is positive)

For a concave lens: P is negative      ( f is negative)

S.I unit of power of lens: Dioptre (D)

Definition of 1 dioptre:

Since P = (1/f)       ∴ when f = 1m,      P = 1/1 = 1 dioptre  

∴ “1 dioptre is the power of a lens whose focal length is 1 metre”

Note:

(i) Power of a lens will be in dioptre if its focal length is in metre.

(ii) Lens Maker’s formula          P = (µ – 1) [1/R₁ – 1/R₂]

# Sign conventions for Lenses:

For convex Lens u → negative f → positive v → positive (For real image) → negative (For virtual image)

For concave Lens Always Virtual image u → negative v → negative f → negative

 

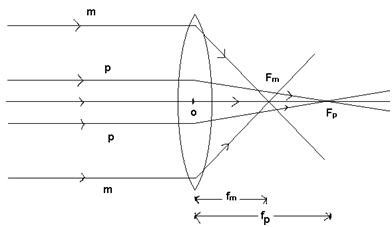
# Spherical aberration in Lenses:

“The inability of a lens to focus all the rays of light falling on it a single point”

Paraxial Rays:

The rays of light close to principal axis of a lens are called as paraxial rays.

Marginal Rays:

The rays of light which are for away from the principal axis of a lens are called as marginal rays.

# Combination of lenses:

“When two or more then lenses are combined, then total magnification produced by the combination is equal to the product of the magnifications produced by each lens.”

i.e. m = m₁ x m₂ x m₃ x……….

# Focal lengths for a lens combination:

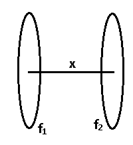
(a) When two thin lenses are at a finite distance:

1/f = 1/f₁ + 1/f₂ – x/f₁ f₂

P = P₁ + P₂ – x P₁ P₂                         

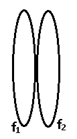
(b) When two thin lenses are in contact:

1/f = 1/f₁ + 1/f₂       (x = 0)

P = P₁ + P₂                             

_{f → Focal length of the combination.}