# Sign conventions for concave & convex mirrors:-

Concave M	Convex M
1. Object distance                  u → -ve 2. Image distance                   v → -ve (Real image)                                                    → +ve (virtual) 3. Focal length                        f → -ve 4. Radius of curvature           R → -ve 5. Height of object                O → +ve 6. Height of real image         I → -ve 7. Height of virtual image    I → +ve	1. Object distance       u → -ve 2. Image distance        v → +ve 3. Focal length              f → +ve 4. Radius of curvature R → +ve 5. Height of object       O → +ve 6. Height of real image I → +ve (virtual)

# Mirror formula (using concave mirror):-

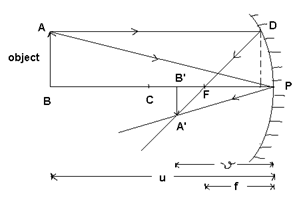
(i) When the object is placed beyond the centre of curvature (Real image)

Consider an object AB placed beyond the centre of curvature of a concave mirror of small aperture.

Δ’S A’B’F and DNF are similar;

∴ A’B’/DN = FB’/NF = FB’/PF              s

Or       A’B’/AB = PB’ – PF/PF                ( DN = AB NF ≈ PF)

Using sign conventions; PB’ = -v

PF = -f

∴ A’B’/AB = -v – (-f)/-f = v – f/f = v/f – 1               — (1)

Parallel by Δ’S A’B’P and ABP are similar;

∴ A’B’/AB = PB’/PB = -v /-u = v/u                            — (2)

From (1) and (2)

v/f – 1 = v/u

Or       1/f – 1/v = 1/u         (dividing both sides by v)

Or       I/u + 1/v = 1/f          (Mirror formula)

u → object distance

v → image distance

f → Focal length

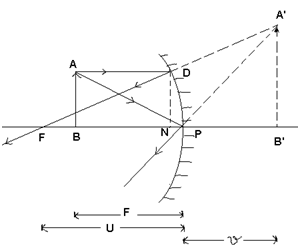
(ii) When the object is place between pole (P) and Focus (F) (Virtual image)

Δ’S A’B’F and DNF are similar;              

∴ A’B’/DN = B’F/NF

Or       A’B’/AB = PB’ + PF/PF   (∵ DN = AB NF ≈ PF)

Using sign conventions, PB’ = +v

∴ A’B’/AB = v – f/-f = f – v/f = 1 - v/f                       — (1)

Parallel by Δ’S A’B’P and ABP are similar;

∴ A’B’ – PB’ = +v              — (2)

∴ m = h₂/h₁ = v/-u      i.e. m is positive

(b) For a convex mirror

A Virtual and erect image is formed (always)

A’B’ = +h₂, AB’ = +h₁

B’P = +v, BP = -u

∴ m = h₂/h₁ = v/-u      i.e. m is positive

Note: when m > 1, image formed is enlarged.

When m < 1, image formed is diminished.

# Other formula for magnification:-

(i) Magnification in terms of u and f,

1/u + 1/v = 1/f

Multiplying both sides by u,

1 + u/v = u/f

u/v = u/f – 1 = u – f/f

v/u = f/u – f

For virtual images in concave and convex mirrors

m = -v/u = f/f – u

(ii) Magnification in terms of v and f

1/u + 1/v = 1/f

Multiplying both sides by v

v/u + 1 = v/f

v/u = v/f – 1 = v – f/f

For virtual image in concave and convex mirrors

m = -v/u = f – v/f

From (1) and (2)

1 – v/f = -v/u

1/v – 1/f = -1/u                (dividing both sides by v)

Or       1/u + 1/v = 1/f (Mirror formula)

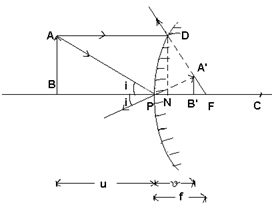
# Mirror formula (using convex mirror)

Consider an object AB placed in front of a convex mirror of small aperture.

Δ’S A’B’F and DNF are similar;

∴ A’B’/DN = B’F/NF

Or       A’B’/AC = PF – PB’/PF                (∵ DN = AB NF ≈ PF)

Using sign conventions; PF = +f

PB’ = +v

∴ A’B’/AB = f – v/f = 1 – v/f                             —(1)

Parallel by Δ’S A’B’P and ABP are similar;

∴ A’B’/AB = PB’/PB = +v/-u                            —(2)

From (1) and (2)

1 – v/f = -v/u

Or       1/v – 1/f = -1/u                    (dividing both sides by v)

Or       1/u + 1/v = 1/f