# Radioactivity:- It is the phenomenon of spontaneous disintegration of the nucleus of an atom with the emission of one or more penetrating radiation like ∝ particles, β particle or γ particles.

The substance which spontaneously emit penetrating radiation were called radioactive substances. For example: Uranium, Colonium, Radium, Thorium, Actinium, etc

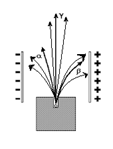
Becquerel Rays (Electrical nature of Radioactive Radiation)

In both the cases the narrow beam splits into three components.

1. The component which bend towards the left consist of positively charged particle called ∝-Rays.

2. The component which bend towards right consist of negatively charged particles called β-Rays.

3. The components which goes straight consist of neutral phonons are called γ-Rays.    

# Laws of Radio-active disintegration:

Rutherford & Soddy Fazans give the laws of radioactive disintegration substances. This law states that -->

1. The process of radioactive disintegration is completely spontaneous is which the small amount of energy is emitted.   

2. The emission of ∝, β, γ rays does not occur simultaneously from the nucleus, it means that at one time ∝, β, γ rays are emitted.

3. During ∝ decay when one element changes into another element the mass number of the new element decreases by 4 & its atomic number by 2. It is given by

4. During β-decay, the atomic number of the daughter atom increases by 1 & mass number remains same.

Very Very Important

The note of disintegration of a radioactive substance is directly proportional to the number of atom present initially at the sample of the radioactive substance, According to radioactive law

(dN/dt) ∝ N

(dN/dT) = (-λ) N  (-because of disintegration)

Where λ is called decay constant

(dN/N) = (-λ) dt

Integrating both sides we have

= ∫(dN/N) = -λ ∫dt

= log_e N = -λt + C     —(1)

(C is integration constant)

When t = 0, then number of atom N = N_o, then equation

(1) becomes

log_e N_o = -λ (0) + C

C = log_e N_o    —(2)

From equation (1) & (2)

log_e N = -λt + log_e N_o

-λt = log_e N - log_e N_o

log_e N = log_e N_o = -λt

log_e(N/N_o) = -λt

∴ (log m – log n) = log (M/n)

log_e (N/N_o) = -λt

N/N_o = e^-λt

N = N_o e^-λt

This equation represents, the radioactive decay law

==> it gives the number of active nuclei left after time t thus the number of active nuclei in a radioactive substance decreases exponentially with time.

# Half life of Radioactive substance

It is defined as the time is which any radioactive substance after disintegration becomes half of the original quantity. Let N_o is equal to number of radioactive nuclei present in the radioactive same initially at t = 0.

N is equal to number of radioactive nuclei left at any instant i.e. When t = T_1/2, N = N_o/2

Now,

N = N_o e^-λt

Where λ is radioactive decay constant putting above values in this equation.

N_o/2 = N_o e^-λt

Taking logarithm  side the me have

λ. T_1/2 log e^e = log e²

λ. T_1/2 = log e²

T₁/2 = log e²/λ

==> T_1/2 = 2.303 log 10²/λ

==> T_1/2 = 2.303 x 0.3010/λ

T_1/2 = 0.623/λ

Thus half life of λ radioactive substance is inversely ∝ to its decay constant & is independent of the number of N_o the number of radioactive nuclei present initially in the sample.