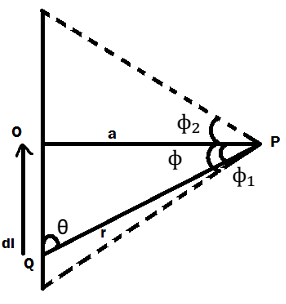
Magnetic field due to a long straight current carrying conductor: As shown in fig. consider straight conductor XY carrying current I. We wish to find its magnetic field at the point P whose perpendicular distance from the wire is a. i.e. PQ = a.

Consider a small current element  of the conductor O. its distance from Q is L. let r be the position vector of point P relative to the current element and θ be the angle between   and  According to Biot – Savart law, the magnitude of the field dB due to the current element dl will be

From right angled triangle, ΔOQP

θ + φ = 90°

θ = 90° - φ

Therefore, sin θ = sin (90 – φ) = cos φ

Also cos φ = a/r

As

l = a tan φ

Differentiating, we get

dl = a sec² φ dφ

Or

According to right hand rule, the direction of the magnetic field at the point P due to all such current element will be in the same direction, normally, into the plane of the paper. Hence total field B at the point P due to the entire conductor is given by

This equation gives magnetic field due to a finite wire in terms of the angles subtended at the observation point by the ends of the wire.

Special Cases:

1. If the conductor XY is infinitely long and point P lies near the middle of the conductor, then φ₁ & φ₂ = π/2

∴ B = μ₀I/4πa (sin 90° + sin 90°)

Or

B = μ₀I/2πa

2. If the conductor XY is infinitely long but the point p lies near the end Y or X

Then φ₁ = π/2, & φ₂ = 0°

Then

B = μ₀I/4πa (sin 90° + sin 0°) = μ₀I/4πa

3. If the conductor is of finite length L and the point P lies on its perpendicular bisector, then φ₁ & φ₂= φ and                            ∴ B = μ₀I/4πa(sin φ + sin φ)       

Direction of magnetic field:

For an infinitely long conductor,

B = μ₀I/2πa

i.e.

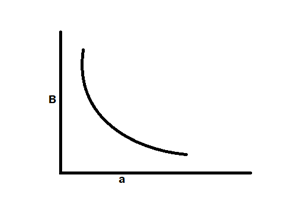
B ∝ 1/a

Clearly, the magnitude of magnetic field will be same at all points located at the same distance from the conductor. The magnetic lines of force of a straight current carrying conductor are concentric circle with the wire at the centre and in a plane perpendicular to the wire.

1. If the current flows upwards, the lines of force have anti clock wise sense.
2. If the current flows downwards, then the lines of force have clock wise sense.

Rules for binding the direction of magnetic field due to a straight current carrying conductor:

(1) Right hand thumb rule: If we hold the straight conductor in the grip of our right hand in such a way that extended thumb point in the direction of current, the direction of curl of finger will give the direction of the magnetic field.

(2) Maxwell’s cork screw rule: If a right handed screw be rotated along the wire so that it advances in the direction of the current, then the direction in which the thumb rotates gives the direction of the magnetic field.

Variation of magnetic field with distance from straight current carving conductor:

As B ∝ 1/a

Graph is a hyperbola.

 

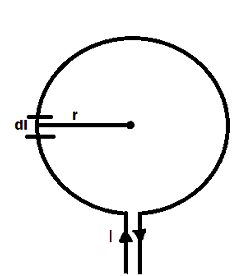
Magnetic field at the centre of a circular current loop:

Consider a circular loop of radius r of current element dl of the loop.

According to Biot-Savart law, the magnetic field at the centre O due to this element is

the field at O points normally in to the plane of paper as shown by encircled cross. Consequently, the magnetic field at the centre O due to this current element is

The total magnetic field at the centre O is

= (µ₀/4π) (I/r²)*2πr= (µ₀/2) (I/r)

For N loops, all wound over one another, then

B = (µ₀/2) (NI/r)       

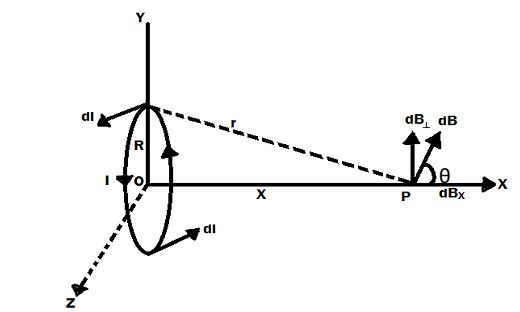
Magnetic field along the axis of a circular current-loop:

Consider a current element dl  at the top of the loop. From Biot-Savart law, the field at point P due to the current element is

dB = (µ₀/4π) (Idlsinθ/s²)  

Let φ be the angle between OP and CP. Then dB can be resolved in to rectangular components

(i) dB Sin φ along the axis

(ii) dB Cos φ along perpendicular to the axis

The total magnetic field at the point P in the direction CP is

B = (µ₀/4π) (Ia/s³)* 2πa

= (µ₀/2) (Ia²/s³)     

Now,

S = (r² + a²)1/2

∴ B = (µ₀/2) (Ia²/(r²+a²)^3/2)      

If coil consists of N turns, then

B = (µ₀/2) (NIa²/(r²+a²)^3/2)      

Special cases:

(1) At the centre of current loop, r = 0, therefore

B = (µ₀/2) (NIa²/a³) = µ₀NI/2a  

Or

B = (µ₀/2) (NI A/πa³), where A = πa², area of circular current loop.

The field is directed perpendicular to the plane of the current loop.

(2) At the axial points lying far away from the coils r>>a, so that

B = (µ₀/2) (NI a²/r³) = (µ₀/2) (NI A/πr³)

The field is directed along the axis of the loop and falls off as the cube of the distance from the current loop.

(3) At an axial point at a distance equal to the radius of the coil

i.e.

r = a, we have  

B = (µ₀/2) (NI a²/(a²+a²)^3/2)  = (µ₀/2) (NI/2(5/2)a)

Rules for finding the direction of a magnetic field due to a circular current loop:

(1) Right hand thumb rule: If we curl the palm of right hand around the circular wire with the fingers pointing in the direction of the current, then the extended thumb gives the direction of magnetic field.

(2) Clock Rule: This rules gives the polarity of any face of the circular current loop. If the current round any face of the coil is in anti clock wise direction. It behaves like a north pole. If the current flows in the clock wise direction, it behaves like a south pole.