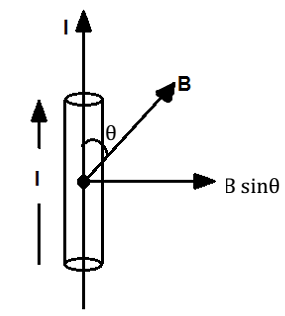
As shown in fig., each electron experiences a magnetic Lorentz force along inward direction , which is given by

If n is the number of free electrons per unit volume, then total number of electrons in the conductor is

N = n*volume = nAL

Total force on the conductor is

But I = enAv_d

_{Or F = lLB sinθ}

Expression for the force between two parallel current carrying wires:

 

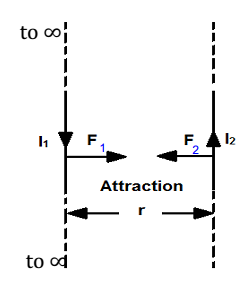
As shown in fig. consider two long parallel wires AB and CD carrying current l₁ and l₂. Let r be the separation between them.

The magnetic field produced by current l₁ at any point on wire CD is B₁ = µ₀I₁/2πr

This field acts perpendicular to the wire CD and points into the plane of paper. It exerts a force on current carrying wire CD. The force acting on length l of the wire CD will be

F₂ = I₂lB₁sin90 = I₂l(µ₀I₁/2πr) = (µ₀I₁I₂/2πr)*l

According to Fleming’s left hand rule, this force acts at right angles to CD, towards AB in the plane of the paper. Similarly, an equal force is exerted on the wire AB by the field of wire CD. Thus when the current in the two wires are in the same direction, the force between them attractive. It can be easily seen that

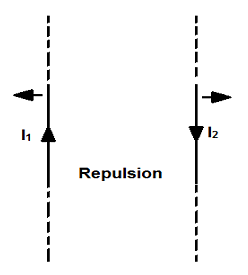
As shown in fig b, when the current in the two parallel wires flow in opposite directions, the force between the two wires are repulsive. Thus, parallel currents attracts each other and antiparallel currents repel.

And if l₁ and l₂ = 1 A and r = 1 m then

f = µ₀/2π = 2 * 10⁷ N/m

“one ampere is that value of steady current, which on flowing in each of the two parallel infinitely long conductors of negiligible cross-section placed in vacuum at a distance of 1 m from each other, produces between them a force of 2 * 10^-7 N/m of their length.