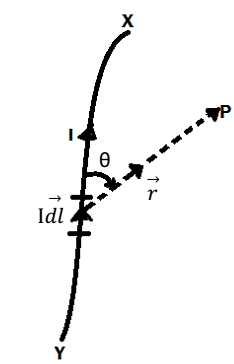
Biot-Savart law: According to Biot-Savart law, the magnitude of the field dB is

1. Directly proportional to the current I through the conductor. i.e. dB ∝ I
2. Directly proportional to the length dl of the current element. i.e. dB ∝ dl
3. Directly proportional to the sinθ, i.e. dB ∝ sinθ
4. Inversely proportional to the square of the distance r of the point p form

the current element, i.e. dB ∝ 1/r²

Combining all these four factors we get

The proportionality constant K depends on the medium between the observation point P and the current element and the system of unit chosen. For free space and in SI units,

µ₀ is the constant called permeability of free space. So

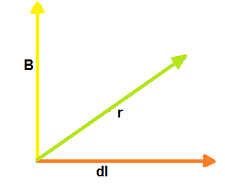
As the direction of dB is perpendicular to the plane of dl and r. so we get the vector from of the Biot - Savart law as

Direction of dB: The direction of dB is the direction of the vector . It is given by right hand screw rule, which states that if we place a right handed screw at point p perpendicular to the plane of the paper and turn its handle from to .

then the direction in which the screw advances gives the direction in which the screw advances gives the direction of dB. Thus the direction  is perpendicular to and into the plane of the paper, as has been shown by encircled cross * at point P in fig.

Special cases:

1. If θ = 0°, sin θ = 0, so that dB = 0. i.e. the magnetic field is zero at points on the axis of the current element.
2. If θ = 90°, sin 90 = 1, so that dB is maximum. i.e., the magnetic field due to a current element is maximum in a plane passing through the element and perpendicular to its axis.

SI unit of magnetic field: The SI unit of magnetic field if Tesla.

According to Biot – Savart law,

If I = 1A, dl = 1m, r = 1 m and θ = 90° so that sin θ = 1 then

Thus one Tesla is 10⁷ times the magnetic field produced by a conducting wore of length one meter and carrying current of one ampere at a distance of one meter from it and perpendicular to it.

Relation between µ_0,ε₀ and c: As we know that

1/4πε₀ = 9* 10⁹ Nm²m^-2

μ₀/4π = 10^-7 T mA^-1 or W bA^-1m^-1

Therefore,

μ₀ ε₀ (μ₀/4π)( 4π ε₀) = 10^-7 * 1/(9*10⁹) = 1/(3*10⁸)² = 1/c²

 Therefore,

 μ₀ ε₀ = 1/c²

or c = 1/( μ₀ ε₀)^1/2, Where c is the velocity of light in vacuum.