Ampere’s Circuital law: The line integral of the magnetic field around any closed circuit is equal to the µ₀ times the total current l threading or passing through the closed circuit.

Mathematically,

. = µ₀I

Proof:

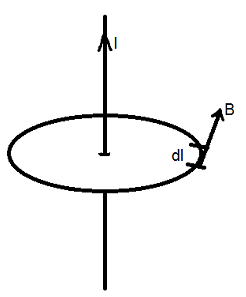
Consider an infinitely long straight conductor carrying a current l. from Biot Savart law, the magnitude

of the magnetic field B due to current carrying conductor at a point, distant r from it is given by

B = µ₀I/2πr

As shown in fig. at every point on the circle B and dl are tangential to the circle so that the angle between them is zero.

Hence the line integral of the magnetic field along the circular path is

. = . = (µ₀I/2πr)l

= (µ₀I/2πr)*(2πr) = µ₀I

∴ . = µ₀I

This proves Ampere’s law

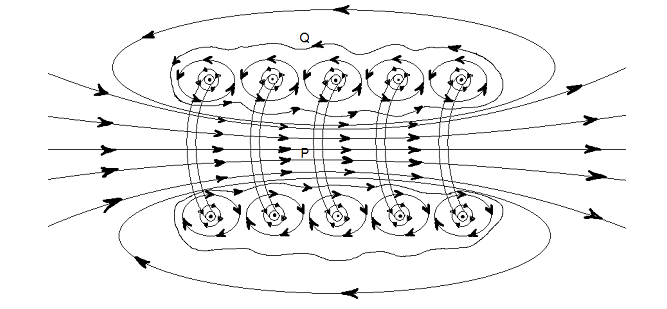
Magnetic field of a straight solenoid: A solenoid means an insulated copper wire wound closely in the form of a helix.

As shown in fig, current enters the plane of paper at points marked x and leaves the plane of paper at points marked. The magnetic field at points close to a single turn of the solenoid is in the form of concentric circles like that of a straight current carrying wire. The resultant field of the solenoid is the vector sum of the field due to all the turns of the solenoid. Obviously the fields due to the neighboring turns up along the axis of the solenoid but they cancel out in perpendicular direction. The field at interior mid – point P is uniform and strong. The field at the exterior mid point Q is weak and is along the axis of the solenoid with not perpendicular component.

Ampere right hand rule:

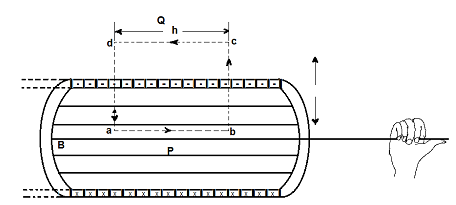
Grasp the solenoid with the right hand so that the fingers point along the direction of the current, the extended thumb will then indicate the face of the solenoid that has north polarity.

Calculation of the magnetic field inside a long straight solenoid:

Consider a rectangular closed path abcd as the amperean loop. According to Ampere’s circuital law,

Ampere right hand rule:

Grasp the solenoid with the right hand so that the fingers point along the direction of the current, the extended thumb will then indicate the face of the solenoid that has north polarity.

Calculation of the magnetic field inside a long straight solenoid:

Consider a rectangular closed path abcd as the amperean loop. According to Ampere’s circuital law,

Now,

But

As B = 0 for all points outside the solenoid.

Where l = length of the side ab of rectangular loop abcd.

Let number of turns per unit length of the solenoid = n

Then number of turns in length l of the solenoid = nl

Thus the current l of the solenoid threads the loop abcd, nl times.

∴ total current threading the loop abcd = nlI

Hence Bl = µ₀nlI

Or B = µ₀nI

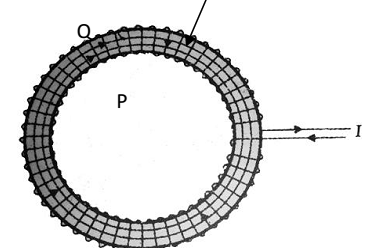
Magnetic field due to a Toroidal solenoid: A solenoid bent in to the form of a closed ring is called a Toroidal solenoid.

(i) For points in the open space interior to the toroid:

Let B, be the magnitude of the magnetic field along the Amperean loop

1 of radius r₁.

Length of the loop1, L₁ = 2πr₁

As the loop encloses no current, so l = 0

Applying Ampere’s circuital law,

B₁L₁ = µ₀I

B₁ * 2πr₁ = µ₀ * 0 = 0

B₁ = 0

Thus the magnetic field at any point P in the open space interior to the toroid is zero.

(ii) For points inside the toroid:

Let B, be the magnitude of the magnetic field along the Amperean loop 2 of radius r.

Length of the loop 2, L₂ = 2πr

If N is the total number of turns in the toroid and l the current in the toroid, then total current enclosed by the loop 2 = Nl

Applying Ampere’s circuital law,

B * 2πr = µ₀NI

B = (µ₀NI/2πr)

If r be the average radius of the toroid and n the number of turns per unit length, then

N = 2πrn

∴ B = µ₀nI

(iii) For points in the open space exterior to the toroid: each turn of the toroid passes twice through the area enclosed by the Amperean loop 3. But for each turn, the current coming out of the plane of the paper is cancelled by the current going in to the plane of paper. Thus, l = 0, and hence B = 0.