Magnetic dipole moment of a revolving electron

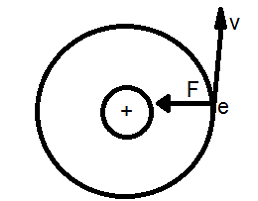
According to Bohr model of Hydrogen like atoms, negatively charged electron revolves around the positively charged nucleus. This uniform circular motion of the electron is equivalent to current loop which possess the magnetic dipole moment = IA

And

Current is I = e/t = e/(2πr/v) = ev/2πr

A = πr² is the area of the current loop.

Then, the orbital magnetic moment of the electron is μ_I = IA = (ev/2πr) πr²

μ_I = evr/2 ----------------------(1)

Also, angular momentum of the electron is

L = M_evr ---------------- (2)

Dividing equation 1 by 2, we get

μ_I/1 =evr/(2/M_evr) = e/2M_e

This is called gyromagnetic ratio and its value is 8.8 * 10¹⁰Ckg^-1.

According to Bohr’s quantization condition, angular momentum

L = nh/2π

∴ μ_I = neh/4πM_e

This equation gives orbital magnetic moment of an electron in n^th orbit.

Bohr magnetron: It is defined as the magnetic moment associated with an electron due to its orbital motion in the first orbit of hydrogen atom. Then

μ_B = μ_I= eh/4πM_e

Then,

μ_B = 9.27 * 10^-24 Am²

And