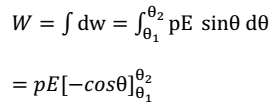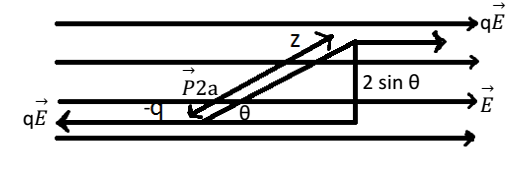
As shown in fig. consider an electric dipole in a uniform electric field E with its dipole moment 'p' making an angle θ with the field. Two equal and opposite forces -qE and +qE acts its two ends. The two forces form a couple. The torque exerted be the couple will be equal to pEsinθ

If the dipole is rotated through a small angle dθ against the torque acting on it then the small work done is

dw = τ dθ = PE sinθ dθ

The total work done in rotating the dipole from its orientation making an angle θ₁ with the direction of field to θ₂ will be

= pE ( cosθ₁ – cosθ₂)

The work done is stored as the potential energy U of the dipole therefore,

U = PE ( cosθ₁ – cosθ₂)

If initially the dipole is oriented perpendicular to the direction of the field (θ₁=90°) and then brought to same orientation making an angle θ₂ = θ with the field then

  U = PE ( cos 90 – cos θ) = - PE cos θ

Special cases:

1. Position of stable equilibrium: when θ = 0⁰

U = - PE cos 0⁰ = PE

Thus the potential energy of a dipole is minimum when its dipole moment is parallel to the external field. This is the position of stable equilibrium.

2. Position of zero energy : when θ = 90⁰

U = - PE cos 90⁰ = 0

Thus the potential energy of a dipole is zero when it is held perpendicular to the external field.

3. Position of unstable equilibrium : θ = 180⁰

U = - PE cos 180⁰ = + PE

Thus the potential energy of a dipole is maximum. When its dipole moment is antiparallel to the external field. This is the position of unstable equilibrium.