Combination of capacitors in series:

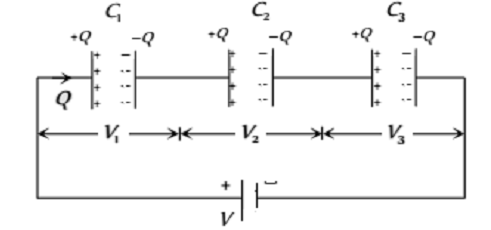
When the –ve plate of 1 capacitor is connected to the positive plate of the second and the –ve of the second to the +ve of third and so on, the capacitor are said to be connected in series. Fig. show three capacitor of capacitance C₁, C₂, C₃ connected in series a potential difference V is applied across the combination this sets up charges ±Q on the two plates of each capacitor. The potential differences across the various capacitor are

V₁ =Q/C₁ ,V₂ =Q/C₂ ,V₃ =Q/C₃

For the series circuit, the sum of these potential differences must be equal to the applied potential difference.

Therefore V = V₁ + V₂ + V₃

As

Where C_s is the equivalent capacitance of the series combination, then

For a series combination of capacitors, the reciprocal of equivalent capacitance is equal to the sum of the reciprocal of the individual capacitances.

Capacitors in parallel: When the positive plates of all capacitors are connected to one common point and the negative plates to another common point, the capacitor are said to be connected in parallel.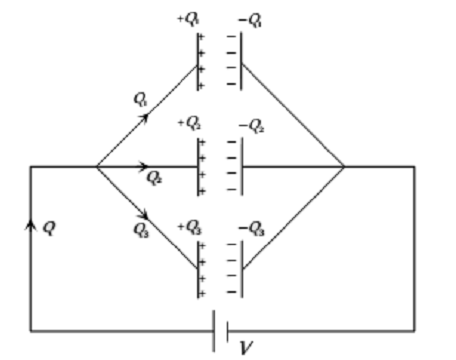

Fig. shows the three capacitor of capacitances C₁, C₂, C₃ connected in parallel. A potential difference V is applied across the combination this sets up and

Q₁ = C₁V,

Q₂ = C₂V,

Q₃ = C₃V.

Total charge stored in the combination is

Q = Q₁ + Q₂ + Q₃ = (C₁ + C₂ + C₃)V

If C_p is the equivalent capacitance of the parallel combination is

Q = C_pV

Then

C_pV = (C₁ + C₂ + C₃)V

C_p = C₁ + C₂ + C₃

Hence for parallel combination of capacitors, the equivalent capacitance is equal to the sum of the individual capacitances.