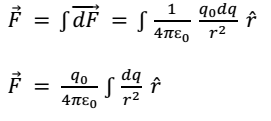Electric field due to a point charge:

As shown in fig. consider a point charge q placed at the origin o. we wish to determine its electric field at a point P at distance r form it. For this, imagine a test charge q₀ placed at point p. according to the coulomb’s law, the force on charge q₀ is

 this means that at all points on the spherical surface drawn around the point charge, the magnitude is same and does not depend on the direction of r. such a field is called spherically symmetric or radial field. i.e. a field which looks the same in all directions when seen from the point charge.

Electric field due to a system of point charges:

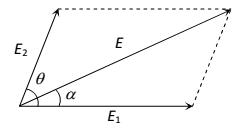
As shown in fig. consider N point charges q₁, q₂, q₃, ………..q_n, place in vacuum at points whose position n vectors w.r.t. origin o are     respectively according to the coulomb’s law the force on charge q₀ due to charge q₁ is  

The electric field at pint p due to charge q₁ is

According to the principle of superposition, the electric field at point P to a system of N charges is

in terms of position vectors,

Continuous Charge Distribution:

In practice, we deal with charges much greater in magnitude than the charge on an electron, so we can ignore the quantum nature of charges and imagine that the charge is spread in a region in a continuous manner. Such a charge distribution is known as continuous charge distribution.

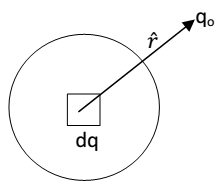
Force on O point charge qo due to continuous charge distribution

As shown in fig. consider a point charge q₀ lying near a region of continuous charge distribution. This continuous charge distribution can be imagined to consist of a large number of small charges dq. According to the coulomb’s law, the force on charge q₀ due to small charge dq is

By the principle of superposition , the total force on charge q₀ will be vector sum of the force exerted by all such small charges and is given by