Postulates of Bohr’s theory of hydrogen atom:

This model also called planetary model of the atom is based on the following postulates:

(i) Nuclear concept: An atom consist of a small massive central core called nucleus around which planetary electrons revolves

The centripetal force required for their rotation is provided by electron static attraction between e^- and the nucleus.

(ii) Quantum condition: of all the possible circular orbits allowed by the classical theory, the electrons are permitted to circulate only in those orbits in the angular momentum of an e^- is on which integral multiple of (h/2π) whose h is u plank’s constant. Therefore, for any permitted orbit.

L = mvr = nh/2π,               n = 1, 2, 3…………

Where n = Principle quantum number

(iii) Stationary orbits: While revolving in the (acceptable) Permissible orbits an electron does not radiate energy. These non radiating orbits are called stationary orbits.

(iv) Frequency Condition: An atom can emit the form of discrete energy photons only when an electron gimps from a higher to the lower orbit or from lower to higher orbit respectively if E₁ and E₂ are the en energies associated with these permitted orbit then the frequency (ν) of the emitted or absorbed radiation is given by     

hν = E₂ – E₁

Bohr’s theory of hydrogen atom: (Radii of permitted (allowed) orbits in the hydrogen atom)

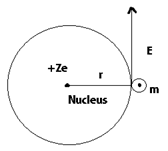
According to Bohr Theory of atom, H atom consist of nucleus with positive charge Z e and a single e^- of charge –e which revolves around the nuclear in a circular orbit of radius r.

Here Z is the atomic number and for hydrogen atom Z = 1, The electrostatic force of attraction between the nucleus and the e^- is

F = K q₁q₂/r₂

F = K Ze.e/r²

F = K. Ze²/r²                        —(1)

To keep the e^- in its orbit, the centripetal force on the e^-  must be equal to the electrostatic, attraction therefore,

mV²/r = K. Ze²/r²                              —(2)

r = K. Ze²/mv²                              —(3)

Where m = mass of the electron and V is its speed in an orbit of radius r. Bohr’s quantization condition for angular momentum is mvr = nh/2π

r = nh/2πmv                       —(4)                 

From equation (3) and (4)

K. Ze²/mv² = nh/2πmv

V = K 2πZe²/nh

Substituting this value of v in equation (4), we have

r = (nh/2πm) (nh/K 2πZe²)

r = n²h²/4π² kmZe²                          —(6)     

as r is proportional to n² the radii of permitted orbits increase in the ratio of 1 : 4 : 9 : 16………

The radius of the innermost orbit of the hydrogen atom called Bohr’s radius and can be determined by putting Z = 1 and n = 1 in equation (6) and it is denoted by r_o. So equation (6) becomes

r_o = n₂/4π²m Ke²

Substituting the value of all the constants

r_o = (6.63 x 10^-34)²/4 x (3.14)² x (9.1 x 10^-31) x 9 x 10⁹ x (1.6 x 10^-19)

r_o = 5.29 x 10^-11 m

= 0.53 A^°