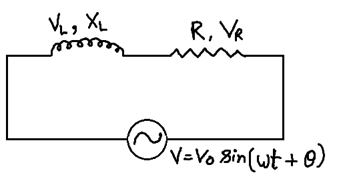
(4) Series LR circuit

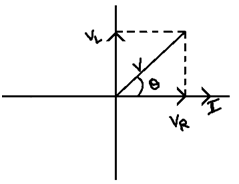
V = (V_R² + V_L²)^1/2     

V_L = I X_L

V_R = I R

V = I Z

V = (V²_R + V²_L)^1/2

I Z = (IR)² + (I X_L)²)^1/2

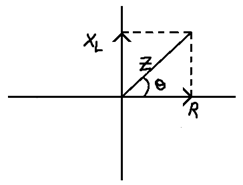
Z = (R² + X²_L)^1/2

Also tanθ = (V_L/V_R) = (I X_L/I R) = X_L/R

Phase difference θ = tan^-1(X_L/R)

The nature of circuit in Inductive as voltage in leading current by angle θ

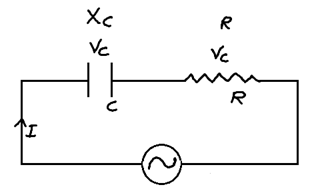
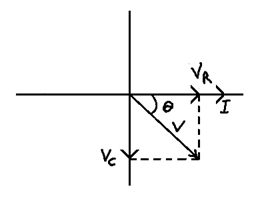
(5) Series CR circuit

V = (V_R² + V_e²)^1/2

tanθ = V_C/V_R

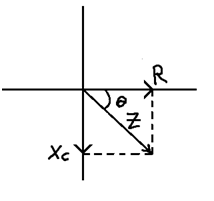
Z = (R² + X_C²)^1/2

tanθ = X_C/R

Phase difference = θ = tan^-1 (X_C/R) or tan^-1 (V_C/V_R)

The nature of circuit is capacitive as voltage is lagging current by angle θ

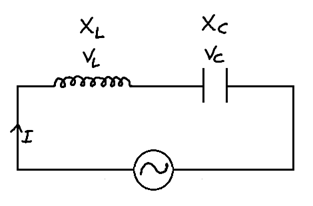
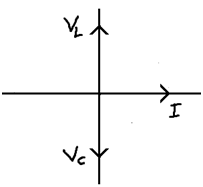
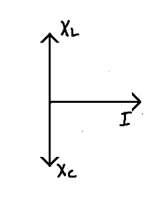
(6) Series LC circuit

V = V_L - V_C θ = +π/2

Or

V = V_C - V_L   θ = -π/2

 

Z = X_L - X_C   θ = +π/2

Or

X_c - X_L   θ = -π/2

When V_L = V_C          Z = 0

Phase angle Arbitrarily

V = I Z

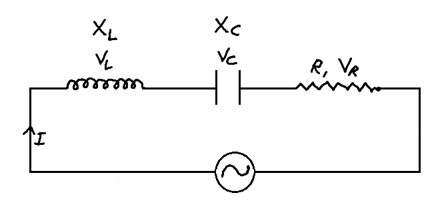
(7) Series LCR circuit

V_L > V_C

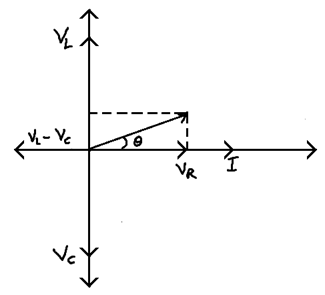
V = (V_R² + (V_L– V_C)²)^1/2

tan θ = (V_C – V_C/V_R)

If V_L > V_C   Inductive nature

V_C > V_L   Capacitive nature

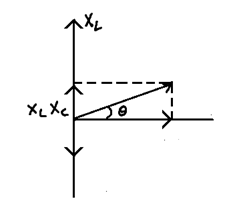
Z = (R² + (X_L – X_C)²)^1/2

tan θ = X_L – X_C/R