Nerst equation of electrode potential (Effect of electrolyte constrictions T)

Electrode potential is said to be standard electrode potential if measured under standard conditions of concentration l temperature. Electrolyte constriction = 1 m and t 298 K. But if constriction and T condition are not standard, then electrode potential comes out to different, obtained using Nerst equation. It deals with the value of reduction potential only.

Mn⁺ + ne^- → M (s)

Concentration cell: - Cells in which two electrodes are of same material but the constriction of the electrolyte in then is different.

E_cell = (0.0591/n) log (C₂ /C₁)

 

Zn|Zn²⁺ (C₁) ||Zn²⁺ (C₂) |Zn

If C₂ > C, EMF = +ve, Reaction takes place. But no net chemical change takes place.

Equilibrium constant for Nerst equation

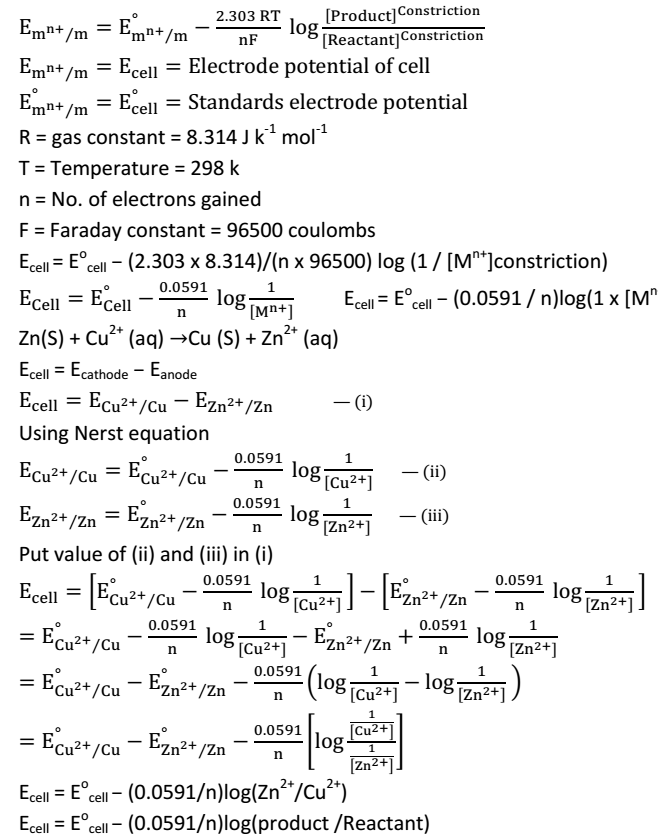
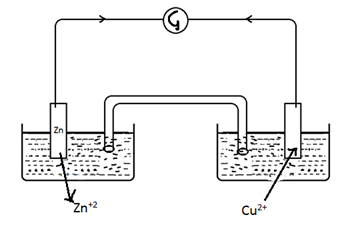
We take example of Zn(s) | ZnSO₄ (aq) ||CuSO₄ (aq) |Cu(s)

Same changes takes place are

• Zn from Zn rod passes into solution So constriction of ZnSo₄ increases
• Cu from CuSo₄ solution deposited on Cu rode constriction of CuSo₄ decreases

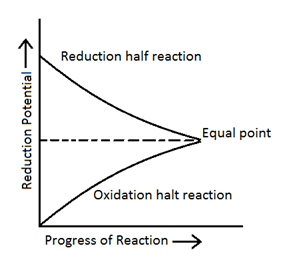
As electrode potential depends upon constriction of solutions, so electrode potential of both electrodes keep on changing as the constriction of both the solution being changing. Ultimately a stage comes when the electrode potential of 2 electrodes becomes equal and current stops flowing in circuit and EMF of cell becomes zero then cell reaction is said to be in equilibrium. So

Zn + CuSo₄ → Cu + ZnSo₄

[Zn²⁺]/ [Cu²⁺] = equilibrium = K_C   

When constriction = K_C, then E_Cell = 0

0 = E^o_Cell – (0.0591/n) log K_C

E^o_Cell – (0.0591/n) log K_C