Integrated rate equation:-  Rate = (-dA/dt) = k[A]

This is the differential rate equation. But this form is not convenient to the determination of rate law and order of reaction so we lntegrate the rate equations which provided the direct relation b/w time, concentration and rate constant.

1. For zero order reaction:- Consider a reaction is of zero order.

A → Products

Rate = (-dA/dt) = k[A]^o

-dA/dt = k

dA = -K dt

Integrate the above equation from 0 to t

∫dA = -K ∫dt

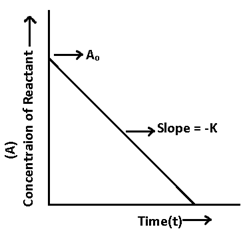
A = -Kt + I      –(1)                I = Integration constant

When t = 0, then A = A_° at initial stages.
Put value of t and A in equation (1)

A_° = -K x 0 + I = I

A_° = I

Put value of I in equation (1)

A = -Kt + A_°              -(2)

Equation (2) is followed by all reactions of zero order

Y = mx =+ c

A = -Kt + A_°

K = 1/t [A_o– A]

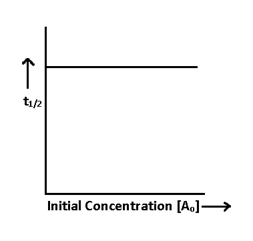
Half life Period:-

It is the time during which the concentration falls to half of the initial concentration.

when t = T_1/2, then [A] = [A]_o/2   

so t = 1/k [A_o – A]

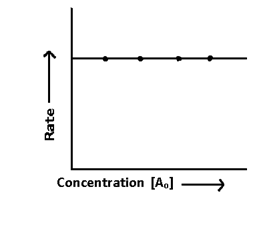
T_1/2∝ Initial concentration or A_o

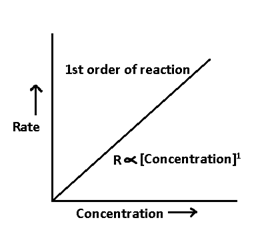
2. for First order reaction:- Consider a reaction of first order

A → product

-dA/dt = k [A]¹       

dA/A = -k dt

Integrate the above equation

∫(dA/A)= ∫ - k dt

 

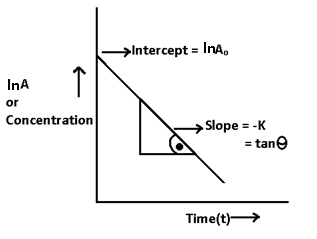
ln A = -Kt + I             -(1)

When t = 0, then A = A_o at initial stages

Put value of t and A in equation (1)

ln A_o = -K x 0 + I

ln A_o = I

Put value of I in equation             -(i)

ln A = -Kt + lnA_o                 -(ii)

Equation (ii) must be followed by al reactions of first order

ln A = -Kt + ln A_o

y = -mx + c

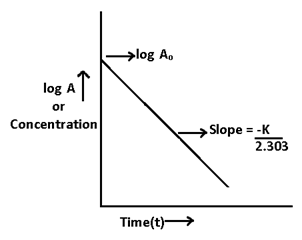
Equation (ii) can also be written as 2.303 log A = -kt + 2.303 log A_o       -(iii)

Divide equation (iii) by 2.303

Log A  = (-kt/2.303) + Log A₀

t = (2.303/k)log(A_o/A)-------(iv)

Half life period:- when t = t_1/2, then A = A_o/2

Put value of t and A In equation (iv)

t_1/2 = 0.693/k

The half life period of first order reaction is independent of initial concentration.

Integrated rate equation for first order gas phase reaction

Consider a gas phase reaction of first order

A → B + C

Initially P_o                 O         O

At time t (P_o - P)      P          P atm

Total pressure of reaction mixture (P_t) = P_o - P + P + P = P_o + P

P = P_t – P_o

Rate of reaction = P_o - P = P_o - P₊ + P_o = 2 P_o - P_t