Theory Part 1
DEFINITION
If a function is one to one and onto from A to B, then function g which associates each element y ∈ B to one and only one element x ∈ A, such that y = f(x), then g is called the inverse function of f denoted by x = g(y).
∴ x = f-1 (y).
If cos θ = x, then θ may be any angle whose cosine is x, and we write θ = cos-1 x. It means that θ is an angle whose cosine is x.
Thus, sin-1 (1) is an angle, whose sine is (1), i.e. θ = sin-1 (1) = n π + (-1)n (π/2)
Where, (π/2) is the least positive value of θ.
The functions sin-1 x, cos-1 x, tan-1 x, cot-1 x, cosec-1 and sec-1 x are called inverse circular or inverse trigonometric functions.
Every inverse circular function is multi-valued. To make each inverse circular function single valued, we define principal value.
Function Domain Range (Principal Values)
sin-1 x [-1, 1] [(-π/2), (π/2)]
cos-1 x [-1, 1] [0, π]
tan-1 x R [(-π/2), (π/2)]
cot-1 x R (0, π)
sec-1 x R-(-1, 1). [0, π] - { π/2}
cosec-1 x R-(-1, 1) [(-π/2), (π/2)] - {0}
Note:
(a) 1st quadrant is common to the range of all the inverse functions.
(b) 3rd quadrant is not used in inverse functions.
(c) 4th quadrant is used in the clockwise direction i.e. -π/2 ≤y ≤0
(d) No inverse function is periodic.
(e) The inverse trigonometric functions are also written arc sinx, arc cosx etc.
GRAPHS OF INVERSE TRIGONOMETRIC FUNCTIONS
1. θ = sin-1 x, where θ ∈ [(-π/2), (π/2)] and x ∈ [-1, 1]
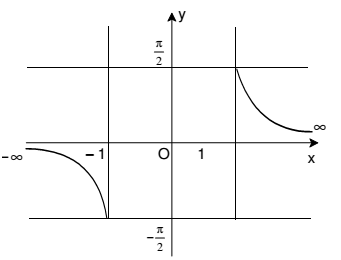
2. θ = cosec-1 x, where θ ∈ and x ∈ (-∞, -1] υ [1, ∞)
Note: cosec-1 x is a decreasing function in (-∞, -1]. It also decreases in [1, ∞)
3. θ = cos-1 x, where θ ∈ [0, π] and x ∈ [-1, 1]
Note: cos-1 x is a decreasing function in [-1, 1]
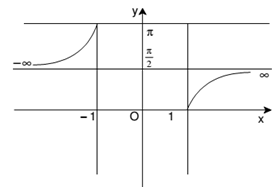
4. θ = sec-1 x, here θ ∈ and x ∈ (-∞, -1] υ [1, ∞)
Note: sec-1 x is an increasing function in (-∞, -1]. It also increases in [1, ∞)
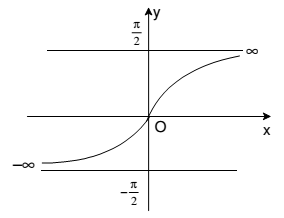
5. θ = tan-1 x, where θ ∈ [(-π/2), (π/2)] and x ∈ [-∞, ∞]
Note: tan-1 x is an increasing function in R.
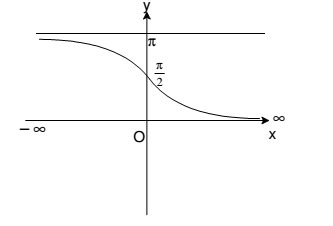
6. θ = cot-1 x, where θ ∈ (0, π) and x ∈ [-∞, ∞]
Note: tan-1 x is an decreasing function in R.
PROPERTIES OF INVERSE TRIGONOMETRIC FUNCTIONS
Property I:
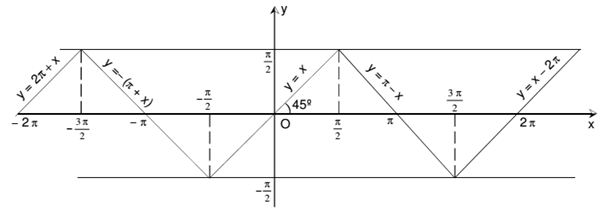
(i) sin-1 (sin x) = x; for all x ∈ [(-π/2), (π/2)]
Let y = sin-1 (sin x), x ∈ R, y ∈ [(-π/2), (π/2)], periodic with period 2π
(ii) cos-1 (cos x) = x; for all x ∈ [0, π] :
Let y = cos-1 (cos x), x ∈ R, y ∈ [0, π], periodic with period 2π
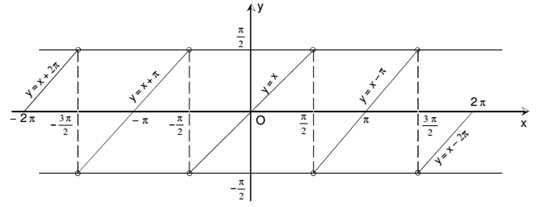
(iii) tan-1 (tan x) = x; for all x ∈ [(-π/2), (π/2)] :
Let y = tan-1 (tan x), x ∈ R –, periodic with period π
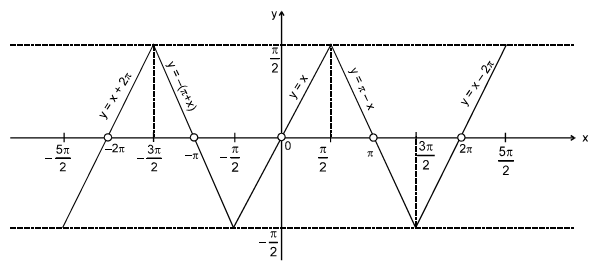
(iv) cosec-1 (cosec x) = x; for all x ∈ [(-π/2), (π/2)], x ≠ for other values of x see the graph:
Let y = cosec-1 (cosec x), x ∈ R, -{nπ, n ∈ I}, y ∈ y is periodic with period 2π
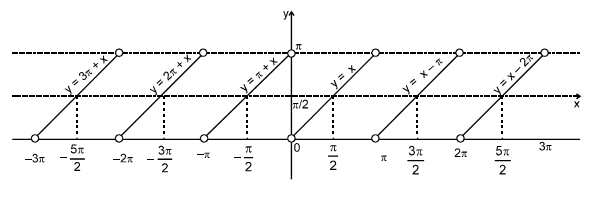
vii) sec-1 (sec x) = x; for all x ∈ [0, π], x ≠ (π/2) for other values of x see the graph:
Let y = sec-1 (sec x), y is periodic; x ∈ R –, with period 2π
(vi) cot-1 (cot x) = x; for all x ∈ (0, π), for other values of x see the graph:
Let y = cot-1 (cot x), x ∈ R - {nπ}, y ∈ (0, π), periodic with π
 SureDen
SureDen