Case 1: If magnitude of Force is and  ፀ is constant

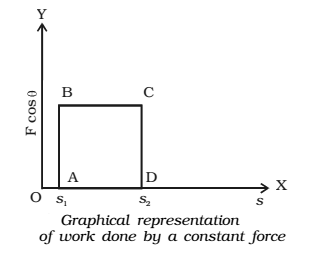
Work Done by a Constant Force.

Let a constant force F be applied on the body such that it makes an angle ፀ with the horizontal and body is displaced through a distance s along horizontal direction.

 F has  two components :

(i) F cosፀ  acts in the direction of displacement of the body.

(ii) F sinፀ  acts in the perpendicular direction of displacement of the body.

Since body is being displaced in the direction of Fcosፀ , no work is done by Fsinፀ and therefore work done by the force in displacing the body through a distance s is given by

    W= F cosፀ s  = Force in the direction of displacement * displacement

or W= F * scosፀ=Force * displacement in the direction of force

Work Done by any  force is equal to the scalar or dot product of the force and the displacement of the body.

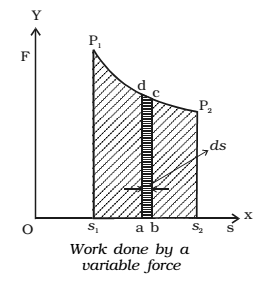
Case 2: If magnitude of Force is variable

If the body is subjected to a varying force F and displaced along X axis  work done

dw = F cos θ. ds = area of the small element abcd.

∴ The total work done when the body moves from s₁  to  s₂  is

Σdw= W = area under the curve P₁P₂= area S₁ P₁ P₂ S₂

_{W = ∫dw = ∫(F cos θ) ds}

So if a force comes to you which is variable like F=2x or F=2t

then you should use integration method to solve questions.

 

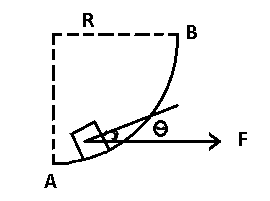
Case 3 If magnitude and direction of force is constant but ፀ is variable

Such questions can be solved using both integration as well as without integration.

In above diagram Force is constant and its direction also but as the block is moved up along the curved portion angle is changing

 

Here in this case curved part is spherical so angle changes from 0 to 90 from as the block is moved from A to B.

Without integration

W= Force * displacement in the direction of  force

W= F * R

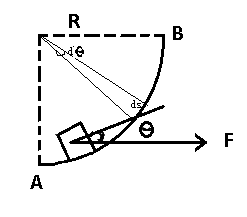
With integration