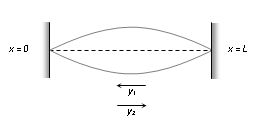
When a string under tension is set into vibration, transverse harmonic waves propagate along its length. When the length of string is fixed, reflected waves will also exist. The incident and reflected waves will superimpose to produce transverse stationary waves in a string

Incident wave y₁ = a sin

According to superposition principle :  y = y₁ + y₂ = 2 a cos

General formula for wavelength  where n = 1,2,3, … correspond to 1^st , 2^nd, 3^rd  modes of vibration of the string.

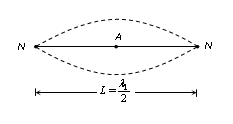
(1) First normal mode of vibration 

This mode of vibration is called the fundamental mode and the frequency is called fundamental frequency. The sound from the note so produced is called fundamental note or first harmonic.

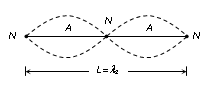
(2) Second normal mode of vibration :

This is second harmonic or first over tone.

(3) Third normal mode of vibration

This is third harmonic or second overtone.

Position of nodes :

For first mode of vibration   x = 0 , x = L                                [Two nodes]

For second mode of vibration x = 0, x =

Position of antinodes :

For first mode of vibration x = L/2                                         [One antinode]

For second mode of vibration x =