Zeroth Law of Thermodynamics.

If systems A and B are each in thermal equilibrium with a third system C, then A and B are in thermal equilibrium with each other.

 

Heat (DQ) : It is the energy that is transferred between a system and its environment because of the temperature difference between them. Heat always flow from a body at higher temperature to a body at lower temperature till their temperatures become equal.

For solids and liquids : DQ = mL    [For change in state]  and  DQ = mcDT  [For change in temperature]

For gases when heat is absorbed and temperature changes :

(DQ)_V = µC_vDT [For constant volume] and (DQ)_P = µC_pDT [For constant pressure]

Work (DW) : Work can be defined as the energy that is transferred from one body to the other owing to a force that acts between them

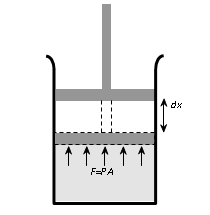
If P be the pressure of the gas in the cylinder, then force exerted by the gas on the piston of the cylinder F = PA

In a small displacement of piston through dx, work done by the gas

                dW = F.dx = PAdx = PdV

Therefore Total amount of work done

(ii) From  DW = PDV = P(V_f – V_i)

                DW = positive if V_f > V_i  i.e. system expands against some external force.

                DW = negative if V_f < V_i  i.e. system contracts because of some external force exerted by the surrounding.

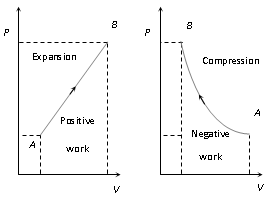
(iii) In P-V diagram or indicator diagram, the area under P-V curve represents work done

W = area under P-V diagram

It is positive if volume increases (for expansion)

It is negative if volume decreases (for compressio

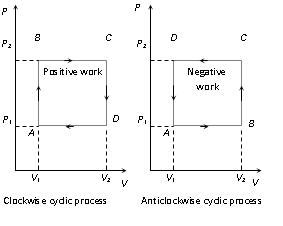
(iv) In a cyclic process work done is equal to the area under the cycle.

It is positive if the cycle is clockwise.

It is negative if the cycle is anticlockwise.

(v)

From this equation it seems as if work done can be calculated only when P-V equation is known and limits V_i and V_f are known to us. But it is not so. We can calculate work done if we know the limits of temperature.

For example, the temperature of n moles of an ideal gas is increased from T₀ to 2T₀ through a process P = α/T  and we are interested in finding the work done by the gas. Then

            PV = nRT                   (ideal gas equation)                       …..(i)

and    P = α/T                                                                               …..(ii)

Dividing (i) by (ii), we get V=nRT²/ α or dV=(2nRT/ α)dT

Therefore

So we have found the work done without putting the limits of volume.

Internal energy (U) : Internal energy of a system is the energy possessed by the system due to molecular motion and molecular configuration.

The energy due to molecular motion is called internal kinetic energy U_K and that due to molecular configuration is called internal potential energy U_P.

i.e. Total internal energy U = U_k + U_p

(i) For an ideal gas, as there is no molecular attraction U_p = 0

i.e. internal energy of an ideal gas is totally kinetic and is given by     

U = U_k=3/2 µRT

and change in internal energy U = 3/2 µRT

(ii) In case of gases whatever be the process

(iii) Change in internal energy does not depends on the path of the process. So it is called a point function i.e. it depends only on the initial and final states of the system, i.e. U = U_f + U_i

(iv) Change in internal energy in a cyclic process is always zero as for cyclic process U_f + U_i

So                   U = U_f + U_i = 0