Adiabatic Process

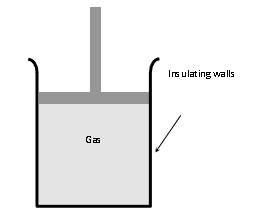
When a thermodynamic system undergoes a change in such a way that no exchange of heat takes place between it and the surroundings, the process is known as adiabatic process.

In this process P, V and T changes but ΔQ = 0.

(1) Essential conditions for adiabatic process

(i) There should not be any exchange of heat between the system and its surroundings. All walls of the container and the piston must be perfectly insulating.

(ii) The system should be compressed or allowed to expand suddenly so that there is no time for the exchange of heat between the system and its surroundings.

Since, these two conditions are not fully realised in practice, so no process is perfectly adiabatic.

(2) Example of some adiabatic process

(i) Sudden compression or expansion of a gas in a container with perfectly non-conducting walls.

(ii) Sudden bursting of the tube of bicycle tyre.

(iii) Propagation of sound waves in air and other gases.

(iv) Expansion of steam in the cylinder of steam engine.

(3) FLTD in adiabatic process : ΔQ = ΔU + ΔW

but for adiabatic process ΔQ = 0    ∴  ΔU + ΔW = 0    

If ΔW = positive then ΔU = negative so temperature decreases i.e. adiabatic expansion produce cooling.

If ΔW = negative then ΔU = positive so temperature increases i.e. adiabatic compression produce heating.

(4) Equation of state : As in case of adiabatic change first law of thermodynamics reduces to,

  ΔU + ΔW = 0,   i.e., dU + dW = 0                           ….. (i)

But as for an ideal gas     dU = µC_vdT and dW = PdV

 

Equation (i) becomes   µC_vdT + PdV = 0                                    ….. (ii)

But for a gas as PV = mRT,  PdV + VdP = µRdT                      ….. (iii)

So eliminating dT between equation (ii) and (iii)   µC_v

_or     [as C_v = R/ (γ-1)]

or  γPdV + VdP=0    i.e.,

Which on integration gives

                      γlog_e V + log_e P = C,       

i.e.,                     log(PV^γ) = C  

or                       PV^γ = constant                                                ….. (iv)

Equation (iv) is called equation of state for adiabatic change and can also be re-written as

TV^γ = constant                               [as P = (mRT/V)]                  ….. (iv)

and     T^γ/P^γ-1=constant                          [as V = µRT/P]             ….. (vi)

(5) Indicator diagram

(i) Curve obtained on PV graph are called adiabatic curve.

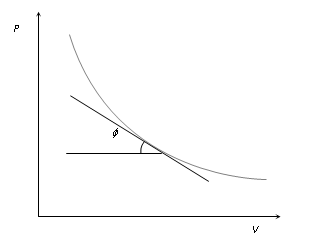
(ii) Slope of adiabatic curve : From PV^γ = constant

By differentiating, we get         dPV^γ + P_γV^γ-1 dV = 0

Therefore      Slope of adiabatic curve tan φ = -γ(P/V)

But we also know that slope of isothermal curve tanφ = -P/V

So,

(6) Specific heat : Specific heat of a gas during adiabatic change is zero

As    C=Q/mΔT=0/m ΔT=0                               [As Q = 0]

7) Work done in adiabatic process

   [As(P=K/V^γ)]

or

or              [As K=PV^γ=P_fV^γ_f=P_iV^γ_i]

or         [As  P_fV_f = µRT_i and P_iV_i= µRT_i ]  

So =

Free expansion : Free expansion is adiabatic process in which no work is performed on or by the system. Consider two vessels placed in a system which is enclosed with thermal insulation (asbestos-covered). One vessel contains a gas and the other is evacuated. The two vessels are connected by a stopcock. When suddenly the stopcock is opened, the gas rushes into the evacuated vessel and expands freely. The process is adiabatic as the vessels are placed in thermal insulating system (dQ = 0) moreover, the walls of the vessel are rigid and hence no external work is performed (dW = 0).

Now according to the first law of thermodynamics dU = 0

If U_i and U_f be the initial and final internal energies of the gas

then       U_f – U_i = 0                             [As  U_f – U_i]

Thus the final and initial energies are equal in free expansion.

 Special cases of adiabatic process

       and Therefore

Type of gas
Monoatomic g = 5/3
Diatomic g = 7/5
Polyatomic g = 4/3

Comparison between isothermal and adiabatic process

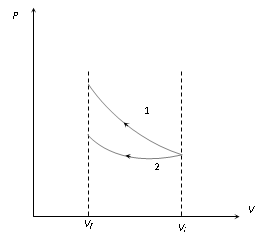
(i) Compression : If a gas is compressed isothermally and adiabatically from volume V_i to V_f then from the slope of the graph it is clear that graph 1 represents adiabatic process where as graph 2 represent isothermal process.

that graph 1 represents adiabatic process where as graph 2 represent isothermal process.

Work done	Wadiabatic > Wisothermal
Final pressure	Padiabatic > Pisothermal
Final temperature	Tadiabatic > Tisothermal

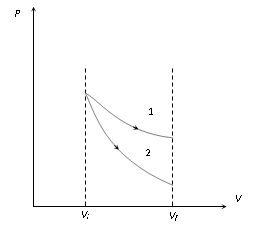
(ii) Expansion : If a gas expands isothermally and adiabatically from volume V_i to V_f then from the slope of the graph it is clear that graph 1 represent isothermal process, graph 2 represent adiabatic process.

Work done	Wisothermal > Wadiabatic
Final pressure	Pisothermal > Padiabatic
Final temperature	Tisothermal > Tadiabatic