Translatory and Rotatory Equilibrium

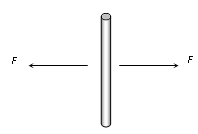
Forces are equal and act along the same line.		ΣF = 0  and Στ = 0	Body will remain stationary if initially it was at rest.
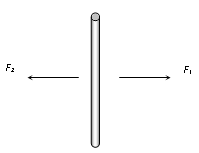
Forces are equal and does not act along the same line.		ΣF = 0  and Στ ≠ 0	Rotation i.e. spinning.
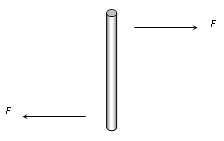
Forces are unequal and act along the same line.		ΣF ≠ 0  and Στ = 0	Translation i.e. slipping or skidding.
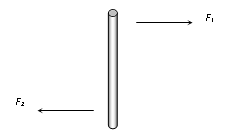
Forces are unequal and does not act along the same line.		ΣF ≠ 0  and Στ ≠ 0	Rotation and translation both i.e. rolling.

 

Equilibrium of bodies and types of equilibrium

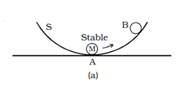
If a marble M is placed on a curved surface of a bowl S, it rolls down and settles in equilibrium at the lowest point A. This equilibrium position corresponds to minimum potential energy. If the marble is disturbed and displaced to a point B, its energy increases when it is released, the marble rolls back to A. Thus the marble at the position A is said to be in stable equilibrium.

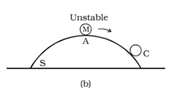
Suppose now that the bowl S is inverted and the marble and the marble is placed at its top point, at A. If the marble is displaced slightly to the point C, its potential energy is lowered and tends to move further away from the equilibrium position to one of lowest energy. Thus the marble is said to be in unstable equilibrium.

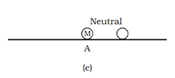
Suppose now that the marble is palced on a plane surface (fig. c). If it is displaced slightly, its potential energy does not change. Here the marble is said to be in neutral equilibrium.

Equilibrium is thus stable, unstable or neutral according to whether the potential energy is minimum, maximum or constant.

We may also characterize the stability of a mechanical system by noting that when the system is disturbed from its position of equilibrium, the forces acting on the system may

1. Tend to bring back to its original position of potential energy is a minimum, corresponding to stable equilibrium.
2. Tend to move it farther away if potential energy is maximum, corresponding unstable equilibrium.
3. Tend to move either way if potential energy is a constant corresponding to neutral equilibrium

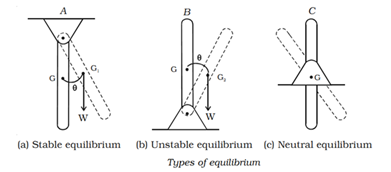
Consider three uniform bars shown in fig. a, b, c. suppose each bar is slightly displaced from its position of equilibrium and then released.

For bar A, fixed at its top end, its centre of gravity G rises to G₁ on being displaced, then the bar returns back to its original position on being released, so that the equilibrium is stable.

For bar B, whose fixed end is at its bottom, its centre of gravity G is lowered to G₂ on being displaced, then the bar B will keep moving away from its original position on being released, and the equilibrium is said to be unstable.

For bar C, whose fixed point is about its centre of gravity, the centre of gravity remains at the same height on being displaced, the bar will remain in its new position, on being released, and the equilibrium is said to be neutral.