Theorem of Parallel Axes

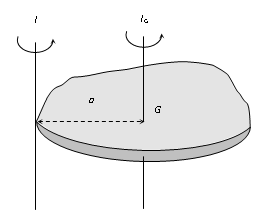
Moment of inertia of a body about a given axis I is equal to the sum of moment of inertia of the body about an axis parallel to given axis and passing through centre of mass of the body I_g and Ma₂ where M is the mass of the body and a is the perpendicular distance between the two axes.

I = I_g + Ma²

Proof:

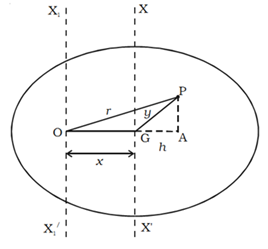
Let us consider a body having its centre of gravity at G as shown in fig. The axis XX’ passes through the centre of gravity and is perpendicular to the plane of the body. The axis X₁X₁’ passes through the point O and is parallel to the axis XX’. The distance between the two parallel axes is x.

Let the body be divided into large number of particles each of mass m. For a particle P at a distance r from O, its moment of inertia about the axis X₁OX₁’ is equal to mr².

The moment of inertia of the whole body about the axis X₁X₁’ is given by,

I₀ = Σmr²                           …. (1)

From the point P, drop a perpendicular PA to the extended OG and join PG.

In the ΔOPA,

OP² = OA² + AP²

r² = (x + h)² + AP²

r² = x² + 2xh + h² + AP²   ….. (2)

But from ΔGPA,

GP² = GA² + AP²

y² = h² + AP²                     …… (3)

Substituting equation (3) in (1),

I_o = Σm (x² + 2xh + y²)

= Σmx² + Σ2mxh + Σmy²

= Mx² + My² + 2xΣmh

Here My² = I_G  is the moment of inertia of the body about the line passing through the centre of gravity. The sum of the turning moments of all the centre of gravity of zero, since the body is balanced about the centre of gravity G.

Σ (mg) (h) = 0    (or)   Σ mh = 0    [since g is a constant]    ….(6)

∴ equation (5) becomes I₀ = Mx² + I_G                 ….. (7)

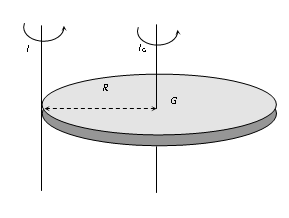
Example: Moment of inertia of a disc about an axis through its centre and perpendicular to the plane is ½ MR², so moment of inertia about an axis through its tangent and perpendicular to the plane will be

I = I_g + Ma²

I = ½ MR² + MR²

∴            I = 3/2 MR²

Theorem of Perpendicular Axes

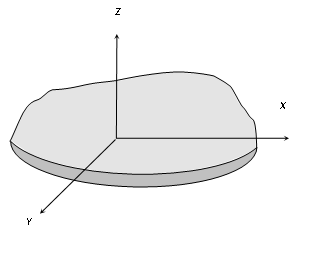
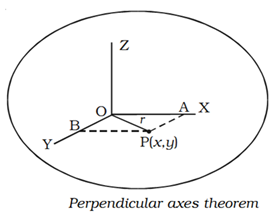
According to this theorem the sum of moment of inertia of a plane lamina about two mutually perpendicular axes lying in its plane is equal to its moment of inertia about an axis perpendicular to the plane of lamina and passing through the point of intersection of first two axes.

I_z = I_x + I_y

 

Proof

Consider a plane lamina having the axes OX and OY in the plane of the lamina as shown fig. the axis OZ passes through O and is perpendicular to the plane of the lamina. Let the lamina be divided into a large number of particles, each of mass m. A particle at P at a distance r from O has coordinates (x,y).

∴ r²  = x² + y²                 ……. (1)

The moment of inertia of the particle P about the axis OZ = mr².

The moment of inertia of the whole lamina about the axis OZ is

I_z = Σ mr²                         ……        (2) 

The moment of inertia of the whole lamina about axis OX is

I_x = Σ my²                        ……        (3)

Similarly, I_y = Σ mx²                    ……        (4)

From equation (2),       I_z = Σmr²= Σm(x² + y²)

I_z = Σmx²+ Σmy²= I_y + I_x

∴ I_z + I_x + I_y

Which proves the perpendicular axes theorem.

Example: Moment of inertia of a disc about an axis through its centre of mass and perpendicular to its plane is 1/2 ½ MR₂, so if the disc is in x–y plane then by theorem of perpendicular axes

i.e.         I_z = I_x + I_y

==>        ½ MR² = 2I_D        [As ring is symmetrical body so I_x = I_y = I_D]

==>        I_D = ¼ MR²

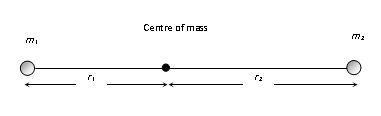
Moment of Inertia of Two Point Masses About Their Centre of Mass

Let m₁ and m₂ be two masses distant r from each-other and r₁ and r₂ be the distances of their centre of mass from m₁ and m₂ respectively, then

(1) r₁ + r₂ = r

(2) m₁r₁ = m₂r₂                    

(3) r₁ = (m₂ / (m₁+m₂)r and r₂ = (m₁ / (m₁+m₂)r

(4) I = m₁r₁² + m₂r₂²

(5) I = [(m₁m₂)/(M₁+m₂)r²  = µr²  [where   [where µ= (m₁m₂)/ (m₁ + m₂) is known as reduced mass µ<m₁ and µ < m₂.]