Rotational kinetic energy and moment of inertia of a rigid body

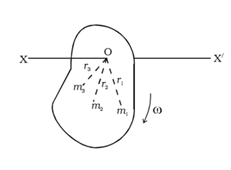
Consider a rigid body rotating with angular velocity about ω about an axis XOX’. Consider the particles of masses m₁, m₂, m₃….. situated at distances r₁, r₂, r₃…. Respectively from the axis of rotation. The angular velocity of all the particles is same but the particles rotate with different linear velocities. Let the linear velocities of the particles be v₁, v₂, v₃… respectively.

Kinetic energy of the first particle = ½ m₁v₁²

But v₁ = r₁ω

∴ Kinetic energy of the first particle

= ½ m₁ (r₁ω)² = ½ m₁r₁²ω²

Similarly, 

Kinetic energy of third particle

= ½ m₃r₃² ω² and so on.

The kinetic energy of the rotating rigid body id equal to the sum of the kinetic energies of all the particles.

∴Rotational kinetic energy

= ½ (m₁r₁²ω²+ m₂r₂²ω²+ m₃r₃²ω²+…… m_nr_n²ω²)

= ½ ω² (m₁r₁²+ m₂r₂²+ m₃r₃²+…… m_nr_n²)

(i.e.) E_R = ½ ω²

In translator motion, kinetic energy = ½ mv²

Comparing with above equation, the inertial role is played by the term

. This is known as moment of inertia of the rotating rigid body about the axis of rotation. Therefore the moment of inertia is

I = mass x (distance)²

Kinetic energy of rotation = ½ ω²I

When ω = 1 rad s^-1, rotational kinetic energy

= E_R = ½ (1)²I               (or) I = 2E_R

It shows that moment of inertia of a body is equal to twice the kinetic enrgy of a rotating body whose angular velocity velocity is one radian per second.