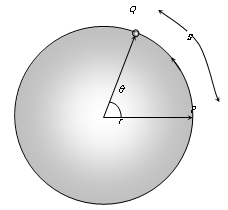
Angular Displacement

It is the angle described by the position vector  about the axis of rotation.

Angular displacement (θ) = Linear displacement (s) / Radius (r)

(1) Unit : radian

(2) Dimension : [M⁰ L⁰ T⁰]

(3) Vector form

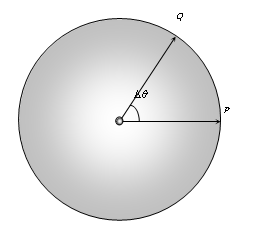
Angular Velocity

The angular displacement per unit time is defined as angular velocity.

If a particle moves from P to Q in time Δt, ω = (Δθ / Δt) where Δθ is the angular displacement.

(1) Instantaneous angular velocity

(2) Average angular velocity ω_av = (Total angular displacement nt/total time)

= (θ₂ – θ₁) / (t₂ – t₁)

(3) Unit : Radian/sec

(4) Dimension : [M⁰L⁰T^-1] which is same as that of frequency.

(5) Vector form [where = linear velocity, = radius vector]

Angular Acceleration

The rate of change of angular velocity is defined as angular acceleration.

If particle has angular velocity ω₁ at time t₁ and angular velocity ω₂ at time t₂ then,

Angular acceleration

(1) Instantaneous angular acceleration

(2) Unit : rad/sec²

(3) Dimension : [M⁰L⁰T^-2].

(4) If α=0, circular or rotational motion is said to be uniform.

(5) Average angular acceleration α_av =( ω₂- ω₁) / (t₂ – t₁).

(6) Relation between angular acceleration and linear acceleration

Equations of Rotational Motion

If angular acceleration α = constant then

1. θ= (( ω₁- ω₂)/2)t
2. α = ( ω₂- ω₁)/t
3. ω₂=( ω₁+ αt)
4. θ= (ω₁t + ½αt²)
5. ω₂²= ω₁² + 2αθ
6. θ_nth = ω₁+ (2n – 1)( α/2)

If acceleration is not constant, the above equation will not be applicable. In this case

1. ω=(dθ/dt)
2. α = (dw/dt)(d²θ/dt²)
3. ωdω= αdθ