Rolling Without Slipping

In case of combined translatory and rotatory motion if the object rolls across a surface in such a way that there is no relative motion of object and surface at the point of contact, the motion is called rolling without slipping.

Friction is responsible for this type of motion but work done or dissipation of energy against friction is zero as there is no relative motion between body and surface at the point of contact.

Rolling motion of a body may be treated as a pure rotation about an axis through point of contact with same angular velocity w.

By the law of conservation of energy

K_N = ½ mv² + ½ Iw²               [∴ As v = Rw]

                                  = ½ mR²w² + ½ Iw²                     

                                  = ½ w²  [mR² +I]

                                 = ½ w² [ I + mR²] = ½ I_Pw²    [As I_P = I + mR²]

 

By theorem of parallel axis, where I = moment of inertia of rolling body about its centre ‘O’ and I_P = moment of inertia of rolling body about point of contact ‘P’.

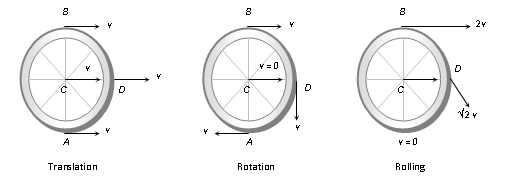
(1) Linear velocity of different points in rolling: In case of rolling, all points of a rigid body have same angular speed but different linear speed.

Let A, B, C and D are four points then their velocities are shown in the following figure.

(2) Energy distribution table for different rolling bodies:

Body	K2/R2	Translatory (KT) ½ mv2	Rotatory (KR) ½ mv2 (K2/R2)	Total  (KN) ½ mv2 (1 + (K2/R2))	(KT/KN) (%)(%)	(KR/KN)(%)
Ring Cylindrical shell	1	½ mv2	½ mv2	mv2	½ (50%)	½ (50%)
Disc solid cylinder	½	½ mv2	¼  mv2	¾  mv2	2/3  (66.6%)	1/3  (33.3%)
Solid sphere	2/5	½ mv2	1/5  mv2	7/10 mv2	5/7 (71.5%)	2/7   (28.5%)
Hollow sphere	2/3	½ mv2	1/3  mv2	5/6 mv2	3/5  (60%)	2/5 (40%)