Radius of Gyration

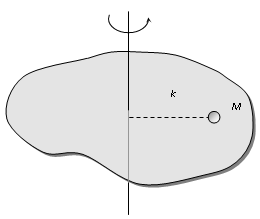
Radius of gyration of a body about a given axis is the perpendicular distance of a point from the axis, where if whole mass of the body were concentrated, the body shall have the same moment of inertia as it has with the actual distribution of mass.

When square of radius of gyration is multiplied with the mass of the body gives the moment of inertia of the body about the given axis.

I = Mk²   or   k = (I/M)^1/2.

    

 

 

Here k is called radius of gyration.

From the formula of discrete distribution

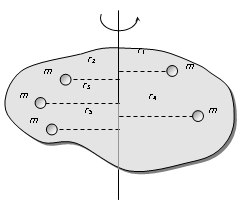
I = mr₁² + mr₂² + mr₃² + ……mr_n²

If m₁ = m₂ = m₃ = ....... = m then

I = m(r₁² + r₂² + r₃² +………. r_n²)       ……..(1)

Fromm the definition of Radius of gyration,

I = Mk²                ………. (ii)

By equating (i) and (ii)

Mk² = m (r₁² + r₂² + r₃² +………. r_n²)

nmk² = m (r₁² + r₂² + r₃² +………. r_n²)    [As M = nm]

∴            k = ((r₁² + r₂² + r₃² +………. r_n²) /n)^1/2

Hence radius of gyration of a body about a given axis is equal to root mean square distance of the constituent particles of the body from the given axis.

(1) Radius of gyration (k) depends on shape and size of the body, position and configuration of the axis of rotation, distribution of mass of the body w.r.t. the axis of rotation.

(2) Radius of gyration (k) does not depends on the mass of body.

(3) Dimension [M⁰L¹T⁰].

(4) S.I. unit: Meter.

(5) Significance of radius of gyration: Through this concept a real body (particularly irregular) is replaced by a point mass for dealing its rotational motion.