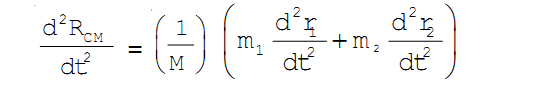Centre of Mass

Centre of mass of a system (body) is a point that moves as though all the mass were concentrated there and all external forces were applied there.

Position vector of centre of mass for two particle system :

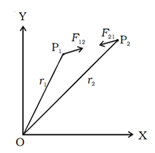
Let us consider a system consisting of two particles of masses m₁ and m₂. P₁ and P₂ are their positions at time t and r₁ and r₂  are the corresponding distances from the origin O as shown fig. Then the velocity and acceleration of the particles are,

v₁ = (dr₁/dt)       ……….(1)

a₁ = (dv₁/dt)       ……….(2)

v₂ = (dr₂/dt)       ……….(3)

a₂ = (dv₂/dt)       ……….(4)

The particle at P₁ experiences two forces:

1. A force F₁₂ due to the particle at P₂ and
2. Force F_1e, the external force due to some particles external to the system.

If F₁ is the resultant of these two forces,

F₁ = F₁₂ + F_1e                      …………(5)

Similarly, the net force F₂ acting on the particle P₂ is, 

F₂ = F₂₁ + F_2e                                ……….. (6)

Where F₂₁ is the force exerted by the particle at P₁ on p₂

By using Newton’s second law of motion,

F₁ = m₁a₁                           ………. (7)

And F₂ = m₂a₂                   ………. (8)

Adding equations (7) and (8), m₁a₁ + m₂a₂ = F₁ + F₂

Substituting, F₁ and F₂ from (5) and (6)

m₁a₁ + m₂a₂ = F₁₂ + F_1e + F₂₁ + F_2e

By Newton’s third law, the internal force F₁₂ exerted by particle at P₂ on the particle at P₁ is equal and opposite to F₂₁, exerted by particle at P₂ on the particle at P₁ is equal opposite to F₂₁, the force exerted by particle at P₁ on P₂.

(i.e.l) F₁₂ = -F₂₁.                ……… (9)

∴ F = F_1e + F_2e                ……….. (10)

[because m₁a₁ + m₂a₂ = F]

Where F is the net external force acting on the system.

The total mass of the system is given by,

M = m₁ + m₂                     …….. (11)

Let the net external force F acting on the system produces an acceleration a_CM called the acceleration of the centre of mass of the system

By Newton’s second law, for the system of two particles,

F = M a_CM                          ………. (12)

From (10) and (12), M a_CM = m₁a₁ + m₂a₂              ……. (13)

Let R_CM be the position vector of the centre of mass.

∴ a_CM = (d² (R_cm) / dt²                ………. (14)

From (13) and (14),

(d²R_CM)/dt²) = (1/M) ((d²/dt²)(m₁r₁ + m₂r₂))

∴ R_CM = (1/M) (m₁r₁ + m₂r₂)

R_CM = (m₁r₁ +m₂r₂) / (m₁ + m₂)            …… (15)

This equation gives the position of the centre of mass of a system comprising two particles of masses m₁ and m₂

If the masses are equal (m₁ = m₂), then the position vector of the centre of mass is, 

R_CM = (r₁ + r₂)/2                          ……… (16)

Which means that the centre of mass lies exactly in the middle of the line joining the two masses.

So Centre of mass is given by

and the centre of mass lies between the particles on the line joining them.

If two masses are equal i.e. m₁ = m₂, then position vector of centre of mass

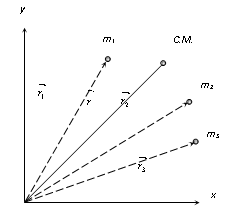
Position vector of centre of mass for n particle system : If a system consists of n particles of masses m₁, m₂, m₃ ……….m_n, whose positions vectors are respectively then position vector of centre of mass

Hence the centre of mass of n particles is a weighted average of the position vectors of n particles making up the system.