Angular Momentum

The turning momentum of particle about the axis of rotation is called the angular momentum of the particle.

or

The moment of linear momentum of a body with respect to any axis of rotation is known as angular momentum. If is the linear momentum of particle and  its position vector from the point of rotation then angular momentum.

Angular momentum is an axial vector i.e. always directed perpendicular to

the plane of rotation and along the axis of rotation.

1. S.I. Unit : kg-m²-s^–1 or J-sec.
2. (2) Dimension : [ML²T^-1] and it is similar to Planck’s constant (h).
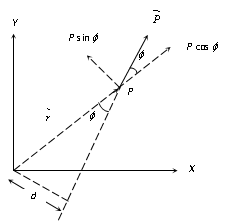
3. As it is clear from the figure radial component of momentum

Transverse component of momentum      

So magnitude of angular momentum L = r P sin

L = r P_φ

\ Angular momentum = Position vector × Transverse component of angular momentum

i.e., The radial component of linear momentum has no role to play in angular momentum.

(4) Magnitude of angular momentum L = P (r sin φ) L = pd  [As d = r sin φ from the figure.]

\ Angular momentum = (Linear momentum) ´ (Perpendicular distance of line of action of force from the axis of rotation)