If a particle is accelerated with constant acceleration in an interval of time, then the motion is termed as uniformly accelerated motion in that interval of time.For uniformly accelerated motion along a straight line, following equations can be used

(a) Ist equation of Motion       

v = u + at                                             

(b) 2^nd equation of Motion          s = ut + (1/2) at²

 x_f = x_i + ut + (1/2) at²        s= x_f - x_i

  (c) 3^rd equation of Motion           v² = u²  + 2as

 (d) Distance covered in nth second s_n = u +( a/2) (2n - 1)

  u = initial velocity (at the beginning of interval)

  a = acceleration

  v = final velocity (at the end of interval)

 s = displacement (x_f - x_i)

 x_f = final coordinate (position)

x_i = initial coordinate (position)

 s_n = displacement during the nth sec

Equations of Kinematics

Ist equation of Motion

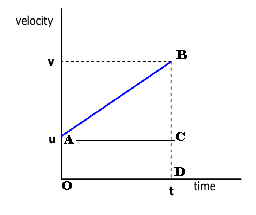
Slope of  Velocity time graph  gives acceleration

Slope= a = BC/AC  = (v- u ) /t

a=(v-u)/t

v- u = at

v= u + at          

1^st equation derived

2^nd Equation of Motion

Displacement= Area under AB

s = Area of  ΔABC + Area of Square ACOD

s = ½ BC x AC + AC x AO

s = ½ (v - u) x t + ut

From 1^st equation

 v – u = at

s = ½ (at) x t + ut

s = ut + ½ at²

 

Third equation of motion.

 

Displacement = Area under AB

= Area of trapezium ABDO

= ½ (sum of parallel sides x shortest distance between parallel sides

= ½ (AO +BD) x AOC

= ½ (u + v) x AC        

 [Also a = BC/AC      AC = BC/a      AC = (v-u)/t   ]

= ½ (u + v) x ((v – u)/a)

s = (v² –u²)/2a

v² – u² = 2as

Derivations using Integration method.

1^st equation of motion.

a = dv/dt              Instantaneous acceleration

dv = a dt

Integrating both sides

[v]_u^v = a [t]_o^t

v – u = a [t - o]

v – u = at

v = u + at

(1^st equation of motion)

 

2^nd equation of motion

Instantaneous velocity = u = ds/dt

u dt = ds

(u + at)dt = ds

u dt + at dt = ds

Integrating both sides

u [t]_o^t + a[t²/2]_o^t = [s]_o^s

u[t - o] + a[t²/2 - o] = s – o

s = ut + ½ at²

 

3^rd equation of motion

We know that a = dv/dt

v = ds/dt

divide s multiply by ds

a = (dv/dt) x (ds/ds) = (dv/ds) x (ds/dt)

a = v (dv/ds)

a ds = vdv

Integrating both sides

a [s]_o^s = [v²/2]_u^v

a [s - o] = [(v²/2) – (u²/2)]

v² – u² = 2as

3^rd equation of motion

 

Distance covered in nth second in a uniformly accelerated motion

Let us consider a particle moving in a straight line with uniform acceleration.

Let u = intial velocity of the particle

a = uniform acceleration of the particle

s_n = distance covered in n seconds

s_n-1 = distance covered in (n -1) seconds

Since     s = ut + ½ at²,

    s_n = un + ½ an²                   (put t = n)

     s_{n – 1} = u (n - 1) + ½ a (n - 1)²         (put t = n - 1)

Clearly,                 s_nth          = s_n – s_n-1

    = [un + ½ an²] – [u(n – 1) + ½ a (n – 1)²]

    = [un + ½ an²] – [ un – u + ½ a(n² + 1 – 2n)]

    = [ un + ½ an²] – [un – u + ½ an² + ½ a – an]

   = u – ½ a + an = u + (a/2) (2n - 1)

Thus,     s_nth = u + (a/2 )(2n – 1)