SWIMMER PROBLEMS

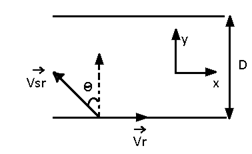
Consider a river of width D.

Let         V_r= velocity of system

Or           velocity of flow or water current

Or           velocity of river 

               V_s = velocity of swimmer/boat with respect to ground.

              V_sr = velocity of swimmer with respect to river or velocity of swimmer in still water.

Now,

Velocity of swimmer along flow or at x-axis = V_r - V_sr sin θ

Velocity of swimmer perpendicular to flow or at y-axis = V_sr cos θ

Time to cross the river: Motion equation at y-axis, t = (D/V_sr cos θ)

This time will be minimum, when cos θ is maximum

cos θ (max) = 1

θ = 90^°

Hence time taken by swimmer is minimum when he steers himself perpendicular to the direction of flow of river.

t_min = (D/V_sr)

Horizontal Drift: It is the distance travelled by swimmer in the direction of flow of river during the time in which he crosses the river.

X = (V_r - V_sr sin θ)t

X = (V_r - V_sr sin θ) (D/ V_sr cos θ)

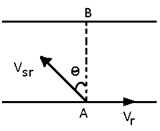
Condition to reach directly opposite point: To reach at point B, X = 0

(V_r - V_sr sin θ) (D/ V_sr cos θ) = 0

sin θ = (V_r/ V_sr)                                                

θ = sin^-1 (V_r/ V_sr)  

We know that sin θ ≤ 1 but here sin θ < 1 because if sin θ = 1 i.e. θ = 90^° then it becomes impossible to cross the river

∴ (V_r/ V_sr) < 1

V_sr > V_r

It means swimmer can reach directly at opposite bank only when his speed in still water must be greater than the flow speed.

Minimum Horizontal Drift: There are two possible cases for X_min.

Case I: V_sr > V_r

In this case X_min = 0

 Case II: V_sr < V_r

X = (V_r - V_sr sin θ) (D/ V_sr cos θ)

For X_min = (dX/dθ) = 0

sin θ = (V_sr/ V_r) ⟹ θ = sin^-1 (V_sr/ V_r)

In this case

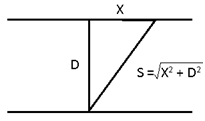
Shortest Path: Path will be shortest when drift will be minimum

Case I: X_min = 0                  i.e. V_sr > V_r

               S_min = D

Case II: When X_min = (1/V_sr) (V²_r – V²_sr)^1/2 D i.e. V_sr < V_r

S_min = (V_r/V_sr)D