Horizontal range : It is the horizontal distance travelled by a body during the time of flight.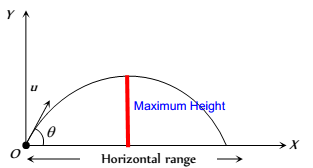

So by using second equation of motion along X axis

x=u_xt + (1/2)a_xt²

x=R , u_x=ucos?  , a_x=0   ,t=T

so

=

 

The maximum range of projectile occurs at θ =45^o and is given by

R_max = (u²/g)

• The ranges are equal for complementary angles of projections,

That is,                  R = (u² sin2θ₁/g)=(u² sin2θ₂/g)

If             θ₁ + θ₂ = 90^o        (complementary angle)

• Furthermore, same ranges also occur for angles symmetrically located about the angle equal to 45^o,

i.e.          θ₁ = 45^o + β

and        θ₂ = 45^o – β

• For complementary angles of projection if T1 and T2 are the respective times of flight then,

T₁T₂ = 2R/g

Range Along the Inclined Plane

The range of the projectile along the inclined plane is given by

R’ = v_||T – ½ a_||T² 

Since     T = (2v_?/a_?) = (2v_o sinθ/g cos α)

                R’ = (2v_o²/g)(sinθcos(θ+α)) / cos² α

Important Points:

• The minimum range occurs when

θ =((π/4) –(α/2))    

 

• The maximum range along the inclined plane when the projectile is thrown upwards is given by

R’_max = (v_o² / g(1+sin α))

• The maximum range along the inclined plane when the projectile is thrown downwards is given by

R’’_max = (v_o² / g(1-sin α))

 

Maximum Height: Applying 3^rd equation of motion along Y axis

v_y² =   u_y² + 2 a_ys_y

v_y=0   , u_y= u sin?   , a_y=-g  s_y­ =H

(0)² – (u sin?)² = 2(-g)H

H=(u sin?)²/2g

In general, H = (v_?² / 2a_?)

 If a projectile is thrown up an inclined plane, as shown in the figure , the maximum height attained is given by