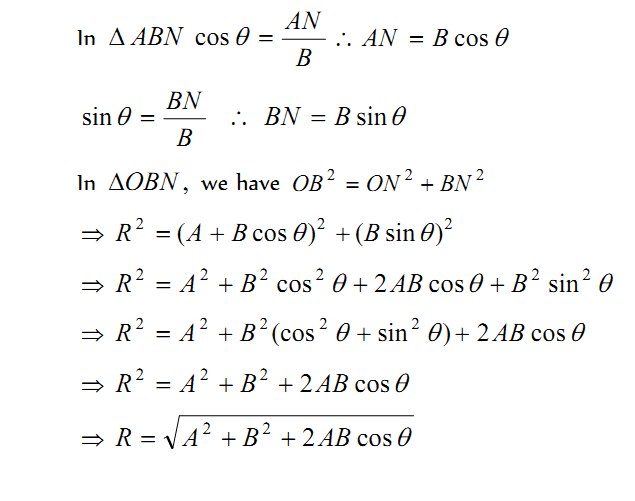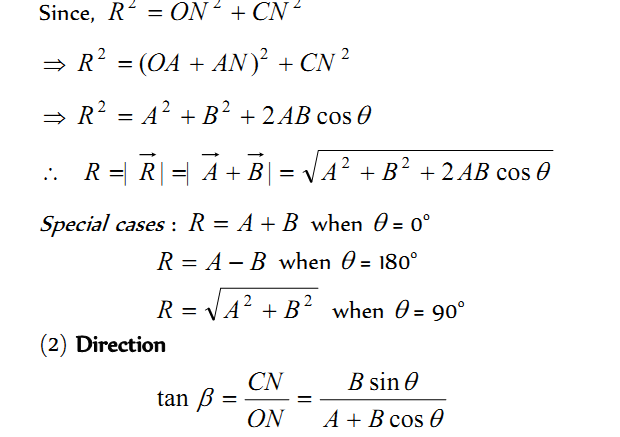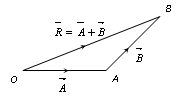
Triangle Law of Vector Addition of Two Vectors.

If two non zero vectors are represented by the two sides of a triangle taken in same order then the resultant is given by the closing side of triangle in opposite order. i.e.

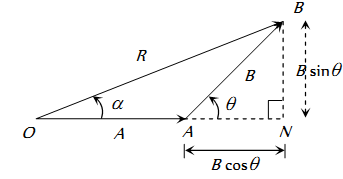
(1) Magnitude of resultant vector

Direction of resultant vectors : If  is angle between     then

If Resultant R makes an angle α  with vector A  then in ∆OBN  then

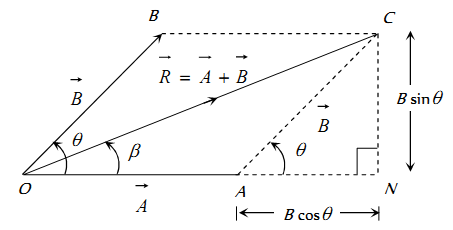
Parallelogram Law of Vector Addition of Two Vectors.

 If two non zero vector are represented by the two adjacent sides of a parallelogram then the resultant is given by the diagonal of the parallelogram passing through the point of intersection of the two vectors.

(1) Magnitude 

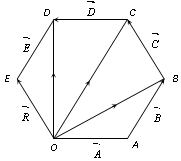
Polygon Law of Vector Addition.

If a number of non zero vectors are represented by the  (n – 1) sides of an n-sided polygon then the resultant is given by the closing side or the n^th side of the polygon taken in opposite order. So,

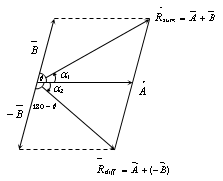
Subtraction of Vectors.

Since,

and 

so  

Since,  cos(180 - θ)  =- cos θ

Important points

(i) A vector can be added to a vector only if they are of same type. For example, velocity can be added to velocity only. Force cannot be added to velocity.

(ii) Minimum number of non-zero unequal vectors whose resultant vector is zero in a plane = 3.

(iii) Minimum number of non-zero vectors in space having resultant zero = 4

(iv) If resultant of two equal vectors has a magnitude equal to magnitude of one vector, then angle between the vectors is 120^°.

(v) The vector does not change due to translation or rotation of reference frame although its components may change.

(vi) Subtraction of two vectors follow from addition as

(vii) i.e., vector subtraction is anti-commutative.

(viii) are perpendicular to each other.