We know that a liquid assumes the shape of the vessel in which it is contained i.e. it can not oppose permanently any force that tries to change its shape. As the effect of force is zero in a direction perpendicular to it, the free surface of liquid at rest adjusts itself at right angles to the resultant force.

When a capillary tube is dipped in a liquid, the liquid surface becomes curved near the point of contact. This curved surface is due to the resultant of two forces i.e. the force of cohesion and the force of adhesion. The curved surface of the liquid is called meniscus of the liquid.

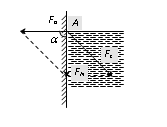
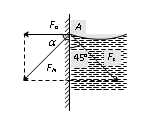
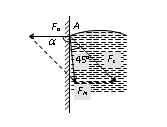
If liquid molecule A is in contact with solid (i.e. wall of capillary tube) then forces acting on molecule A are

(i) Force of adhesion F_a (acts outwards at right angle to the wall of the tube).

(ii) Force of cohesion F_c (acts at an angle 45^o to the vertical).

Resultant force F_N depends upon the value of F_a and F_c.

If resultant force F_N make an angle a with F_a.

Then

By knowing the direction of resultant force we can find out the shape of meniscus because the free surface of the liquid adjust itself at right angle to this resultant force.

 

If    tana =       \ a = 90o i.e. the resultant force acts vertically downwards. Hence the liquid meniscus must be horizontal.	tan a = positive    a is acute angle i.e. the resultant force directed outside the liquid. Hence the liquid meniscus must be concave upward.	tan a = negative   a is obtuse angle i.e. the resultant force directed inside the liquid. Hence the liquid meniscus must be convex upward.
Example: Pure water in silver coated capillary tube.	Example: Water in glass capillary tube.	Example: Mercury in glass capillary tube.