(1) Translatory equilibrium : When a body of density P and volume V is immersed in a liquid of density O, the forces acting on the body are

Weight of body

acting vertically downwards through centre of gravity of the body.

Upthrust force = acting vertically upwards through the centre of gravity of the displaced liquid i.e., centre of buoyancy.

 

If density of body is greater than that of liquid       Weight will be more than upthrust so the body will sink

If density of body is equal to that of liquid       Weight will be equal to upthrust so the body will float fully submerged in neutral equilibrium anywhere in the liquid.

If density of body is lesser than that of liquid                 Weight will be less than upthrust so the body will move upwards and in equilibrium will float partially immersed in the liquid Such that, Þ  Where  is the volume of body in the liquid

Important Points

 (i) A body will float in liquid only and only if

(ii) In case of floating as weight of body = upthrust

So

= Actual weight  – upthrust = 0

(iii) In case of floating

So the equilibrium of floating bodies is unaffected by variations in g though both thrust and weight depend on g.

(2) Rotatory Equilibrium : When a floating body is slightly tilted from equilibrium position, the centre of buoyancy B shifts. The vertical line passing through the new centre of buoyancy B¢ and initial vertical line meet at a point M called meta-centre. If the meta-centre M is above the centre of gravity the couple due to forces at G (weight of body W) and at  (upthrust) tends to bring the body back to its original position. So for rotational equilibrium of floating body the meta-centre must always be higher than the centre of gravity of the body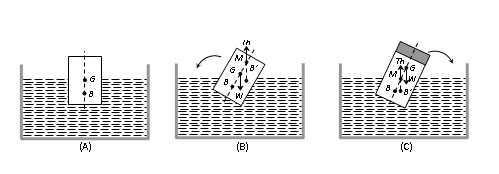

However, if meta-centre goes below CG, the couple due to forces at G and  tends to topple the floating body.

That is why a wooden log cannot be made to float vertical in water or a boat is likely to capsize if the sitting passengers stand on it. In these situations CG becomes higher than MC and so the body will topple if slightly tilted.

(3) Application of floatation

(i) When a body floats then the weight of body = Upthrusti.e., Fraction of volume outside the liquid  If two different bodies A and B are floating in the same liquid then

(iii) If the same body is made to float in different liquids of densities Oa  and Ob respectively.

(iv) If a platform of mass M and cross-section A is floating in a liquid of density  with its height h inside the liquid

Now if a body of mass m is placed on it and the platform sinks by y then

Subtracting equation (i) and (ii),

So we can determine the weight of a body by placing it on a floating platform and noting the depression of the platform in the liquid by it.