The equation of continuity is derived from the principle of conservation of mass.

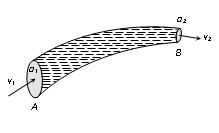
      A non-viscous liquid in streamline flow passes through a tube AB of varying cross section. Let the cross sectional area of the pipe at points A and B be A1 and A2 respectively. Let the liquid enter with normal velocity V1 at A and leave with velocity V2 at B. Let P1 and P2 be the densities of the liquid at point A and B respectively.        

      Mass of the liquid entering per second at A = Mass of the liquid leaving per second at B

This expression is called the equation of continuity for the steady flow of an incompressible and non-viscous liquid.

      (1) The velocity of flow is independent of the liquid (assuming the liquid to be non-viscous)

      (2) The velocity of flow will increase if cross-section decreases and vice-versa. That is why :    

      (a) In hilly region, where the river is narrow and shallow (i.e., small cross-section) the water current will be faster, while in plains where the river is wide and deep (i.e., large cross-section) the current will be slower, and so deep water will appear to be still.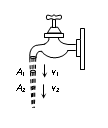

(b)  When water falls from a tap, the velocity of falling water under the action of gravity will increase with distance from the tap (i.e, ). So in accordance with continuity equation the cross section of the water stream will decrease (i.e.,  i.e., the falling stream of water becomes narrower.