11 Bernoulli's Theorem.

According to this theorem the total energy (pressure energy, potential energy and kinetic energy) per unit volume or mass of an incompressible and non-viscous fluid in steady flow through a pipe remains constant throughout the flow, provided there is no source or sink of the fluid along the length of the pipe.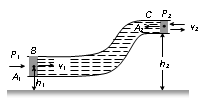

Mathematically for unit volume of liquid flowing through a pipe.

To prove it consider a liquid flowing steadily through a tube of non-uniform area of cross-section as shown in fig. If P1 and P2 are the pressures at the two ends of the tube respectively, work done in pushing the volume V of incompressible fluid from point B to C through the tube will be

This work is used by the fluid in two ways.

(i) In changing the potential energy of mass m (in the volume V ) from mgh₁ to mgh₂,

(ii) In changing the kinetic energy from

This equation is the so called Bernoulli's equation and represents conservation of mechanical energy in case of moving fluids.

(i) Bernoulli's theorem for unit mass of liquid flowing through a pipe can also be written as:

is called velocity head. From this equation Bernoulli's theorem can be stated as.

In stream line flow of an ideal liquid, the sum of pressure head, gravitational head and velocity head of every cross section of the liquid is constant.