Orbital Velocity of Satellite.

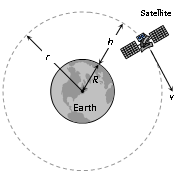
Orbital velocity of a satellite is the velocity required to put the satellite into its orbit around the earth.

 

For revolution of satellite around the earth, the gravitational pull provides the required centripetal force.

                        (m ν²/r) = (GMm/r²)

      ν = (GM/r)^1/2

               ν = (gR²/(R+H))^1/2 = R(g/(R+h)^1/2                [As Gm = gR² and r = R + H]

Note:

(a) Orbital velocity is independent of the mass of the orbiting body and is always along the tangent of the orbit (b) Orbital velocity depends on the mass of central body and radius of orbit.

 (c) Orbital velocity of the satellite when it revolves very close to the surface of the planet

therefore    [As h = 0 and GM = gR²]

For the earth ν = (9.8 x 6.4 x 10⁶)^1/2 = 7.9 km/s ≈ 8 km/sec  

(d) Close to the surface of planet ν = (GM/R)^1/2                             [As ν_e = (2GM/R)^1/2]

therefore                    ν = (ν_e /(2))^1/2 i.e., ν_escape = (2)^1/2 ν_orbital   i.e.,

It means that if the speed of a satellite orbiting close to the earth is made (2)^1/2 times (or increased by 41%) then it will escape from the gravitational field.