Gravitational Potential.

At a point in a gravitational field potential V is defined as negative of work done per unit mass in shifting a test mass from some reference point (usually at infinity) to the given point i.e.,

      [As ]

there fore     I = dV/dr

i.e., negative gradient of potential gives intensity of field or potential is a scalar function of position whose space derivative gives intensity. Negative sign indicates that the direction of intensity is in the direction where the potential decreases.

Note:

 (i) It is a scalar quantity as it is defined as work done per unit mass.

(ii) Unit : Joule/kg or m²/sec²

(iii) Dimension : [M⁰L²T^–2]

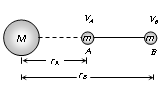
Gravitational potential difference : It is defined as the work done to move a unit mass from one point to the other in the gravitational field. The gravitational potential difference in bringing unit test mass m from point A to point B under the gravitational influence of source mass M is

           ΔV = V_B – V_A = (W_A→B/m)= - GM ((1/r_B) – (1/r_A))

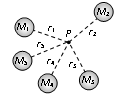
Potential due to large numbers of particles is given by scalar addition of all the potentials.

 V = V₁ + V₂ + V₃ + …………

= - (GM/r₁) – (GM/r₂) – (GM/r₃) ………………….

Gravitational Potential due to a Point Mass using Relation between I and V

If the field is produced by a point mass then           V = - ∫ Idr = - ∫ (-(GM/r²)dr        [As I = -(GM/r²)]

∴                                                                      V = -(GM/r)+c            [Here c = constant of integration]

Assuming reference point at  and potential to be zero there we get

                                                                                    0 = -(GM/∞) + c → c = 0

∴                                  Gravitational potential V = - (GM/r)