Acceleration Due to Gravity.

The force of attraction exerted by the earth on a body is called gravitational pull or gravity.

The acceleration produced in the motion of a body under the effect of gravity is called acceleration due to gravity.

Consider a body of mass m is lying on the surface of earth then gravitational force on the body is given by

             F = GMm/R²                   …..(i)

Where M = mass of the earth and R = radius of the earth.

If g is the acceleration due to gravity, then the force on the body due to earth is given by

                Force = mass ´ acceleration

or                   F = mg                                            …..(ii)

From (i) and (ii) we have mg =GMm/R²

∴                  g = GM/R²                                              …..(iii)

           g = (G/R²) ((4/3) πR³ ρ)                               [As mass (M) = volume ((4/3) πR³) x density (r)]

  there fore                  g = (4/3) πρGR                                       …..(iv)

The value of acceleration due to gravity vary due to the following factors : (a) Shape of the earth, (b) Height above the earth surface, (c) Depth below the earth surface and (d) Axial rotation of the earth.

Variation of g.

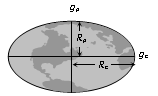
 Variation in g Due to Shape of Earth.

Earth is elliptical in shape. It is flattened at the poles and bulged out at the equator. The equatorial radius is about 21 km longer than polar radius, from g = GM/R²

At equator g_e = GM/R_e²     ......(i)   

         At poles                g_p = GM/R_p²          .....(ii)

         From (i) and (ii) (g_e/g_p) = (R_p²/R_e²)

         Since R_equator > R_pole ∴ g_pole > g_equator and g_p = g_e + 0.018 ms^-2   

Therefore the weight of body increases as it is taken from equator to the pole.

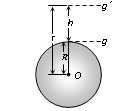
Variation in g With Height.

Acceleration due to gravity at the surface of the earth        

                                    g = GM/R²           .....(i)

Acceleration due to gravity at height h from the surface of the earth   

                                    g’ = GM/(R+h)²    .....(ii)   

From (i) and (ii) g’ = g (R/R+h)²                    .....(iii)

                                                  = g (R²/r²)                      .....(iv)                [As r = R + h]

Note:

 (i) As we go above the surface of the earth, the value of g decreases because g’ ∝ (1/r²).

(ii) If r = ∞ then g’ = 0, i.e., at infinite distance from the earth, the value of g becomes zero.

(iii) If h < < R i.e., height is negligible in comparison to the radius then from equation (iii) we get

                g’ = g (R/R+h)² = g (1 + (h/R))^-2 = g [1 – (2h/R)]                                 [As h < < R]

(iv) If h < < R then decrease in the value of g with height :

                Absolute decrease Δg = g – g’ = (2hg/r)

                Fractional decrease (Δg/g) = ((g - g’)/g) = (2h/R)  

                Percentage decrease (Δg/g) x 100% = (2h/R) x 100%

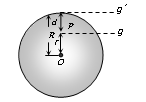
Variation in g With Depth.

Acceleration due to gravity at the surface of the earth

                            g = (GM/R²) = (4/3) πρGR             …..(i)

Acceleration due to gravity at depth d from the surface of the earth

g' = (4/3) πρG(R – d)                       …..(ii)

From (i) and (ii)             g’ = g [1 – (d/R)]

Note:

 (i) The value of g decreases on going below the surface of the earth. From equation (ii) we get g’ ∝ (R – d).

So it is clear that if d increase, the value of g decreases.

(ii) At the centre of earth d = R ∴ g’ = 0, i.e., the acceleration due to gravity at the centre of earth becomes zero.

(iii) Decrease in the value of g with depth

                Absolute decrease Δg = g – g’ = (dg/R)

                Fractional decrease (Δg/g) = ((g-g’)/g) = (d/R)

                Percentage decrease (Δg/g) x 100% = (d/R) x 100%

(iv) The rate of decrease of gravity outside the earth (if h << R) is double to that of inside the earth.