Behavior of Real Gases
Behavior of Real gases (Deviation from ideal behavior)
Ideal gas is that which obeys ideal gas equation PV = nRT under all conditions of temperature and pressure.
No gas is ideal. All gases are real and show deviation from ideal gas behavior
Study of deviation → As PV = const. (Boyle’s law) so graph bet PV (v/s) P should be straight line parallel to x-axis. But real gases don’t show such a behavior.
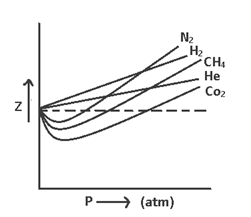
The extent to which a real gas deviates from ideal behavior is studied is terms of compressibility factor ‘Z’ & Z = PV/nRT
For ideal gases, PV = nRT & Z = 1
For real gases, PV ≠ nRT so
(i) Of Z < 1 (ep. CH4, CO2 etc) the gas shows negative deviation i.e. gas is more compressive than expected from ideal behavior.
(ii) Of Z > 1 (ep. H2, He etc) the gas shows positive deviation i.e. gas is less compressive than expected from ideal behavior.
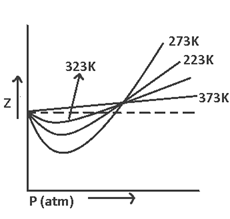
The curve of Z (v/s) P for N2 at different temperatures indicate that at high temperature & low pressure the value of Z approaches = 1. i.e. behavior ideally
Boyle temperature or Boyle point → It’s the temperature at which a real gas behaves like an ideal gas over an appreciable range of pressure.
Significance of Z → Z = (PVreal/nRT) (i) of gas shows
Ideal behavior then PVideal = nRT i.e. Videal = nRT/P
So from equation (i) Z = Vreal/Videal
Cause of deviation from ideal behavior:- At low temperature and low pressure. The gases behave ideally & at low temperature & high pressure ideal behavior.
(i) The volume occupied by gas molecules is negligible in compassion to total volume of gas.
(ii) The force of attraction & or repulsion between gas molecules is negligible.
At low T & high P → (i) The actual mol of gas is not negligible in compassion to total volume.
(ii) The force of attraction or repulsion is not negligible.
Equation of state for the real gases → (Vander Waal’s equation) → (in 1873)
(P + a/V2) (V – b) = RT for 1 mol of gas
(P + an2/V2) (V – nb) = nRT (for n moles of gas)
Deviation of Vander Waal’s equation →
Correction for volume →
Suppose volume of gas molecule = v
Effective volume = b = 4 x v (excluded volume)
So volume of gas = V – b (for 1 mol)
V – nb (for n moles)
Correction for pressure → The molecule colliding with the half of container is attracted by other molecules so it exerts lessee pressure.
So corrected pressure = P + þ
Þ ∝ (density)2 but d ∝ (1/V) or d ∝ (n/V)
(1 mol) (n moles)
So Þ ∝ (1/V2) (1 mole)
Þ = a/V2
Þ ∝ (n2/V2) (for n moles)
Þ = (an2/V2)
Where a → constant
In Vander Waal’s equation,
(P + an2/V2) (V – nb) = nRT
‘a’, & ‘b’, are Vander Waal’s constant their significance is
‘a’ → Greater the value of ‘a’ for a gas greater is the magnificence of attractive forces between gas molecules. & more easily the gas is liquefiable.
‘b’ → It is a measure of effective size of gas molecule greater the value of ‘b’ higher is the size of gas molecules.
Units of ‘a’ As P = (an2/V2) or a = (PV2/n2) = atm. L2 mol-2 or bar dm6 mol-2
Units of ‘b’ As v = nb or b = v/n = L mol-1 or dm3 mol-1
Explanation of behavior of real gases by V.W equation
(i) At very low pressure → V is very large, (a/V2) = small
b → neglected so PV = RT the gas behaves ideally.
(ii) At Moderate pressure → V = small (a/V2) = large
V → still larger than b so
(P + a/V2) (V) = RT or PV + (a/V) = RT
Or PV = RT – (a/V)
Or (PV/RT) = 1 – (a/RTV)
Or Z = 1 – (a/RTV) i.e. Z < 1
(iii) At Greater P → V → very small, (a/V2) large but P is more
So (a/V2) neglected, but ‘b’ can’t be neglected
So P(V – b) = RT or PV – Pb = RT
Or PV = RT + Pb or (PV/RT) = 1 + Pb i.e. Z > 1
Is negligible i.e. a → very = 2 small (a/V2) = negligible
So P(V – b) = RT or Z > 1 & increases with increases is value of P at constant P.
 SureDen
SureDen