Torque on current loop in a uniform magnetic field:

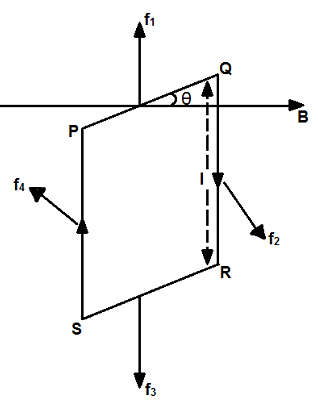
As shown in fig. Consider a rectangular coil PQRS suspended in a uniform magnetic field , with its axis perpendicular to the field.

Let I = current flowing through the coil PQRS

a, b = sides of the coil PQRS

A = ab, area of the coil

θ = angle between the direction of B and that of the vector  drawn normal to the plane of the coil.

Now, a current carrying conductor experiences a force in a magnetic field.

therefore force on side PQ   

 

Its magnitude is

f₁ = laB sin(90-0) = IaB cosθ

therefore force on side QR

Its magnitude is   

f₂ = lbB sin90 = IaB

therefore force on side RS

 

Its magnitude is    

F₃ = laB sin(90+0) = IaB cosθ

therefore force on side SP

Its magnitude is

F₄ = lbB sin90 = IbB

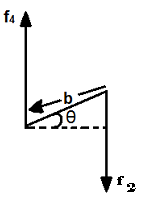
The magnitude of the torque is

  

= lbB * a sinθ = IBA sinθ

   

Where m = lA = magnitude of the magnetic dipole moment.

In vector form

In rectangular loop has N turns, the torque increases N times

τ=NBIAsinθ