# New Cartesian sign conventions:

(i) All the distance are measured from the optical centre of lens.

(ii) The distances measured in the direction of incident light are takes as positive whereas those measured in a direction.

(iii) Height measured above the principal axis is taken positive whereas that measured below the principal axis is taken as negative.

# Lens Maker’s formula

It is the relation between refractive index of the material of a lens, radii of curvature & focal length.

Assumptions to drive lens Maker’s formula:

(i) Thickness of the lens is very small.

(ii) The aperture of the lens is small.

(iii) The object lying on the principal axis is a point

(iv) The incident ray and refracted ray make small angles with the principal axis of the lens.

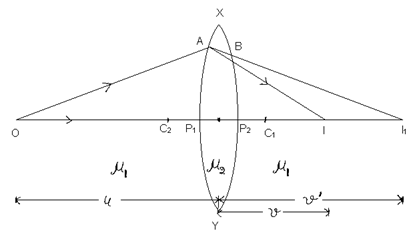
(a) Derivation for convex lens

Let o → Point object lying on the principal axis of a thin convex lens.

µ₂ → Refractive index of the material of the lens

µ₁ → Refractive index of the surrounding medium of the lens (µ₂ > µ₁)

P₁, P₂ → Poles of the two refracting surfaces x P₁Y & x P₂Y

C₁, C₂ → Centres of curvature of refracting surfaces x P₁Y & x P₂Y

R₁ R₂ → Radii of curvature of refracting surfaces x P₁Y & P₂Y

Refraction at surface x P₁Y:

It we assume the absence of surface x P₂Y, then a real image I, is formed in a medium of refractive index µ₂.

For refraction at x P₁Y, we can write:

(-µ₁/u) + (µ₂/v₁) = (µ₂ - µ₁/R₁)                 —(1)

u = OP₁ ≈ OC

v = P₁I₁ ≈ CI₁

Refraction at x P₂Y:

The image at I, acts as a virtual object lying in a medium of refractive index µ₂ and a real image is formed at I.

For refraction at surface x P₂Y, we can write:

-µ₂/v¹ + µ₁/v = (µ₁ - µ₂/R₂)                         —(2)

v¹ = P₂I₁ ≈ CI₁

v = P₂I ≈ CI

(i) + (2) ==>

µ₁/v - µ₁/u = (µ₂ - µ₁) [1/R₁ - 1/R₂]

Or       µ₁[1/v – 1/u] = (µ₂ - µ₁) [1/R₁ - 1/R₂]

Or       (1/v – 1/u) = (µ₂ - µ₁/µ₁) [1/R₁ - 1/R₂] = (µ₂/µ₁ – 1) [1/R₁ – 1/R₂]

Or       (1/v – 1/u) = (¹µ₂ – 1) [1/R₁ – 1/R₂]

(3) µ₂/µ₁ = µ → Refractive index of the material of the lens w.r.t. surrounding medium.

When the object lies as ∞, the image is formed at the focus

i.e. when u = ∞, v = f

∴ (i/f – 1/infinite) = (¹µ₂ – 1) [1/R₁ – 1/R₂]

Or       (1/f = (¹µ₂ – 1) [1/R₁ – 1/R₂]

(4) “Lens Maker’s formula” comparing (3) and (4), we get = (1/f = 1/v - 1/u) Lens formula

(b) Derivation for concave lens:

Let o → Point object lying on the principal axis of the concave lens.