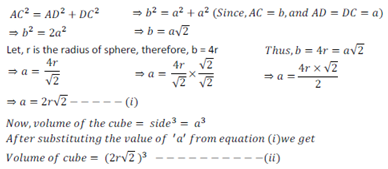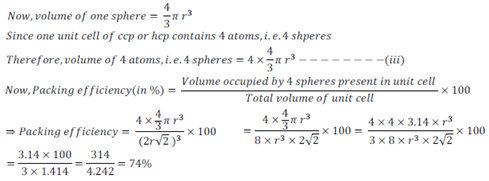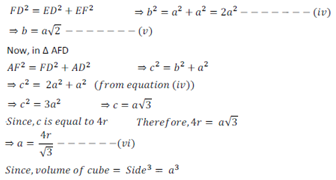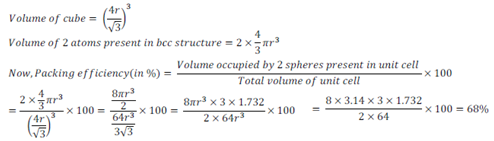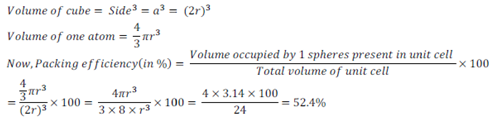Packing Efficiency of Close Packed Structure - 1

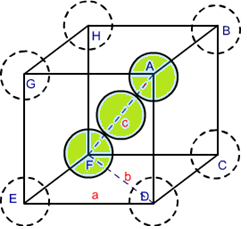
Both ccp and hcp are highly efficient lattice; in terms of packing. The packing efficiency of both types of close packed structure is 74%. The hcp and ccp structure are equally efficient; in terms of packing.

The packing efficiency of simple cubic lattice is 52.4%. And the packing efficiency of body centered cubic lattice (bcc) is 68%.

Calculation of packing efficiency in hcp and ccp structure:

The packing efficiency can be calculated by the percent of space occupied by spheres present in a unit cell.

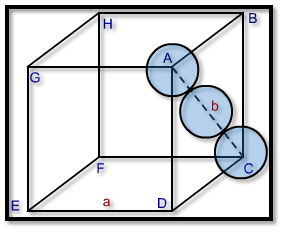
Let the side of an unit cell = a

And diagonal AC = b

Now, in ∆ ABC,

AB is perpendicular, DC is base and AC is diagonal

Thus,packing efficiency of hcp or ccp structure=74%
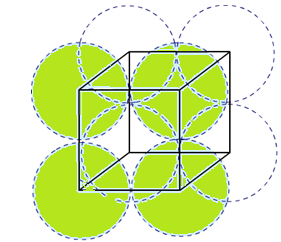
Packing efficiency of body centered cubic (bcc) structure:

In body centered cubic unit cell, one atom is present in body center apart from 4 atoms at its corners. Therefore, total number of atoms present in bcc unit cell is equal to 2.

Let a unit cell of bcc structure with side a.

Let FD (diagonal) = b and diagonal AF = c

Let the radius of atom present in unit cell = r

Now, in ∆EFD

After substituting the value of a from equation (vi) we get

Thus, packing efficiency of bcc structure=68%

Packing Efficiency of Close Packed Structure - 2

Packing efficiency in Simple Cubic Lattice:

A unit cell of simple cubic lattice contains one atom.

Let the side of a simple cubic lattice is ‘a’ and radius of atom present in it is ‘r’.

Since, edges of atoms touch each other, therefore, a = 2r

Thus, packing efficiency of bcc structure=52.4%